espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
les dés du diable
mis à jour le 06/05/2020
Travailler l’approche fréquentielle des probabilités et aborder pour la première fois une approche plus théorique des probabilités
mots clés : probabilité, modélisation
Cette activité est inspirée d’une vidéo de Bernard Delyon (Chercheur au centre Henri Lebesgue) : https://www.lebesgue.fr/fr/video/5min/delyon
Contexte
Classes concernées : 2 classes de 4ème.
Durée de la séance : 3h avec des ordinateurs et des dés à disposition.
Objectifs : travailler l’approche fréquentielle des probabilités et aborder pour la première fois une approche plus théorique des probabilités.
Enoncé
| Vous disposez de 3 dés. Règle du jeu 1/ le 1er joueur choisit un dé. 2/ le 2ème joueur choisit un des 2 dés restants. 3/ Les 2 joueurs lancent leur dé. Celui qui obtient le plus grand score a gagné. Le déroulements des parties Vous jouez contre votre prof de maths préféré. Il est tellement sympa qu'il vous laisse choisir votre dé. Quel dé est-il le plus judicieux pour vous de choisir ? | 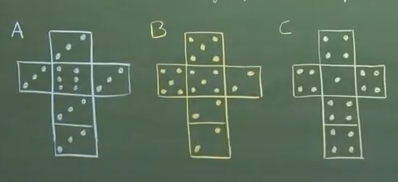 |
Déroulement de l'activité

Les élèves lisent l’énoncé et par groupe de 4 se mettent d’accord sur le choix du dé. C’est déjà l’occasion de premiers échanges et argumentations du style « le dé A gagne moins que le dé C parce que 4 est plus grand que 3 … oui mais quand le dé A tombe sur 6 il gagne toujours » ou « on a une chance sur deux d’avoir 5 avec le dé B et dans ce cas on gagne sur le dé C et si on tombe sur 2 avec le dé B on peut quand même gagner si le dé C fait 1, donc on a plus que la moitié des chances de gagner avec le dé B par rapport au dé C »
2ème temps : recueil des choix des groupes.
Dans mes 2 classes, la moitié des groupes a choisi le dé B et une moitié le dé C. Aucun groupe n’a choisi le dé A.
3ème temps : Justifier nos choix.
Pour se mettre d’accord entre le dé B et le dé C les élèves ont très rapidement l’idée de tester. Pour cela je leur ai fourni les dés.
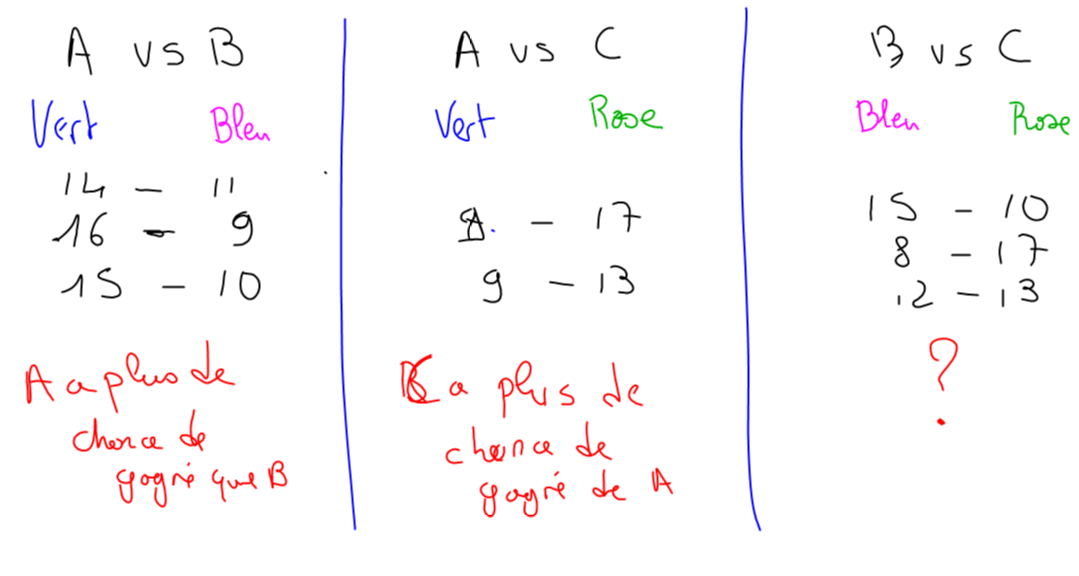 | Une discussion s’engage sur le nombre de lancers à effectuer ; dans chaque classe on réussit à se mettre d’accord sur un nombre de lancers pour qu’il ne soit « ni trop petit, ni trop grand » ; c’est 25 qui est retenu dans les 2 classes. Ci-contre les résultats obtenus dans l’une des classes : Les résultats n’étant pas convaincants, ils décident de soit faire plus de lancers soit d’utiliser le tableur. Je leur explique qu’ils peuvent effectivement utiliser le tableur mais qu’ils peuvent aussi utiliser scratch (et je précise qu’il s’agit de la même difficulté). Quelques soient leurs choix (faire de nouveaux lancers ou programmer) ils finissent tous, au bout d’un certain temps, par utiliser l’ordinateur avec une majorité d’élèves qui choisissent Scratch. |
La modélisation numérique
Je demande donc aux élèves de tout d’abord programmer le dé A
Détection du problème.
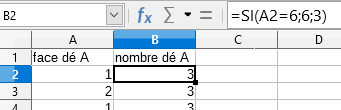
Les élèves comprennent rapidement qu’il faut utiliser « choisir un nombre aléatoire entre … et … » ou « ALEA.ENTRE.BORNE », mais utilisent comme borne 3 et 6 (qui sont les valeurs du dé A). Le problème qu’ils rencontrent c’est que parfois on obtient 4 alors qu’il est sur aucune face du dé. Certains me signalent aussi qu’il faudrait que le 3 apparaisse 5 fois plus souvent que le 6.
Modélisation du problème.
Une discussion s’installe avec toute la classe pour régler le problème. Ils finissent par me dire (en les orientant un peu dans leur réflexion) qu’en numérotant les faces du dé de 1 à 6 et en choisissant une face au hasard, si on tombe sur la face 6 la valeur du dé sera 6 et s’il tombe sur les faces 1,2,3,4 ou 5 la valeur du dé sera 3.
Retour à la programmation
Les élèves finissent par programmer plus ou moins correctement le dé A puis s’attaquent au dé B.
Une deuxième modélisation
Pour le dé B la moitié des groupes a remarqué que l’on avait une chance sur deux d’obtenir5 et une chance sur deux d’obtenir 2. Ils ont donc décidé de modéliser en prenant un aléatoire entre 1 et 2.
Fin de la programmation
3 groupes dans chaque classe ont réussi à programmer la comparaison des dés 2 à 2 (sous scratch) en faisant 100 puis 1000 lancers à chaque fois. En ce qui concerne le tableur seul un groupe (et encore avec de l’aide) a réussi à finir le programme.
Détection du problème.
Les élèves comprennent rapidement qu’il faut utiliser « choisir un nombre aléatoire entre … et … » ou « ALEA.ENTRE.BORNE », mais utilisent comme borne 3 et 6 (qui sont les valeurs du dé A). Le problème qu’ils rencontrent c’est que parfois on obtient 4 alors qu’il est sur aucune face du dé. Certains me signalent aussi qu’il faudrait que le 3 apparaisse 5 fois plus souvent que le 6.
Modélisation du problème.
Une discussion s’installe avec toute la classe pour régler le problème. Ils finissent par me dire (en les orientant un peu dans leur réflexion) qu’en numérotant les faces du dé de 1 à 6 et en choisissant une face au hasard, si on tombe sur la face 6 la valeur du dé sera 6 et s’il tombe sur les faces 1,2,3,4 ou 5 la valeur du dé sera 3.
Retour à la programmation
Les élèves finissent par programmer plus ou moins correctement le dé A puis s’attaquent au dé B.
| Scratch | Tableur |
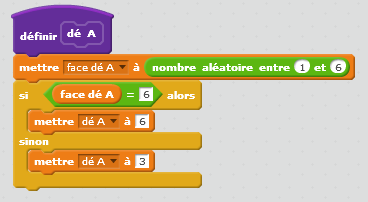 | 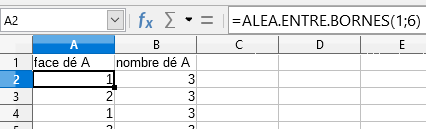  |
Une deuxième modélisation
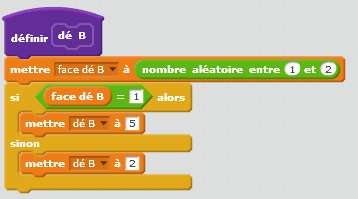
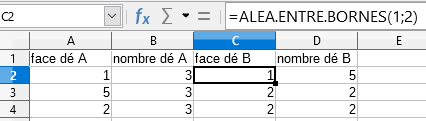
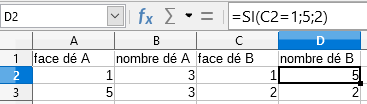
Pour le dé B la moitié des groupes a remarqué que l’on avait une chance sur deux d’obtenir5 et une chance sur deux d’obtenir 2. Ils ont donc décidé de modéliser en prenant un aléatoire entre 1 et 2.
| Scratch | Tableur |
 |   |
Fin de la programmation
3 groupes dans chaque classe ont réussi à programmer la comparaison des dés 2 à 2 (sous scratch) en faisant 100 puis 1000 lancers à chaque fois. En ce qui concerne le tableur seul un groupe (et encore avec de l’aide) a réussi à finir le programme.
| Scratch | Tableur |
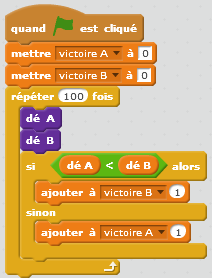 | 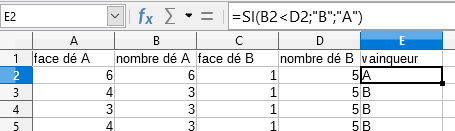 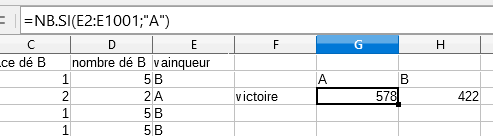 |
La modélisation théorique
Après l’analyse des résultats, nous avons construit ensemble un tableau à double entrées pour déterminer lequel du dé A et du dé B à la plus grande probabilité de gagner.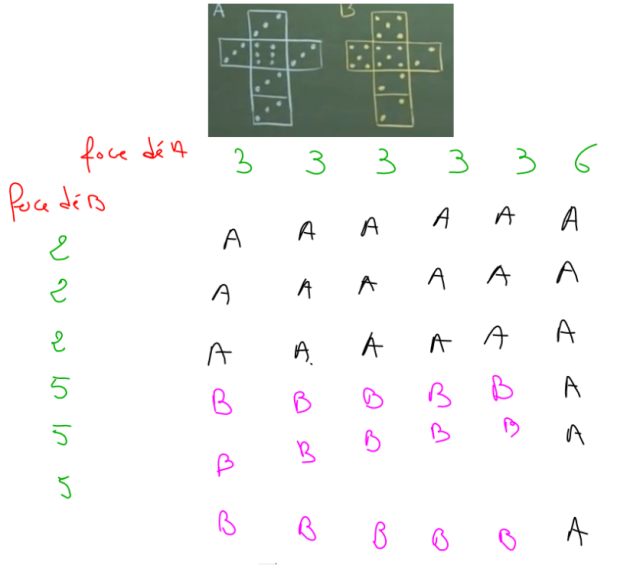
Les élèves ont ensuite fait la même chose avec les dés B et C puis avec les dés A et C.
Les élèves se rendent alors compte que les résultats qu’ils viennent d’obtenir sont cohérents avec ceux qu’ils avaient obtenus lors de la programmation.

Les élèves ont ensuite fait la même chose avec les dés B et C puis avec les dés A et C.
 |  |
Les élèves se rendent alors compte que les résultats qu’ils viennent d’obtenir sont cohérents avec ceux qu’ils avaient obtenus lors de la programmation.
Fin de la séance
Après avoir conclu que le plus malin de tous était le prof car c’est lui qui choisissait le 2ème dé donc il avait toujours plus de chance de gagner. Je leur ai montré la vidéo et ils ont été impressionnés de découvrir les résultats que l’on obtenait quand on lançait 2 fois le dé et que l’on additionnait les résultats des 2 lancers. Certains élèves (très peu mais quand même) ont décidé de le programmer pendant les vacances « pour vérifier que c’était vrai !! ».
Où est la preuve ? Dans le programme ou dans les explications données dans la vidéo, ce sujet fera l’objet d’une autre discussion !
Damien Rivière, Enseignant au collège Pierre Dubois - Laval (53)
information(s) pédagogique(s)
niveau : tous niveaux, Cycle 4, 4ème
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

