espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
optimisation d'une canette
mis à jour le 06/05/2020
mots clés : volume, solide, modélisation
Contexte
Classe concernée : classe de 3ème.
Durée de la séance : 2h avec des ordinateurs à disposition.
Matériel : Il y a dans la classe, à disposition des élèves, des canettes de différents formats, qu’ils peuvent manipuler autant qu’ils veulent.
Enoncé
| Mail reçu par M. Rivière | Extrait du cahier des charge |
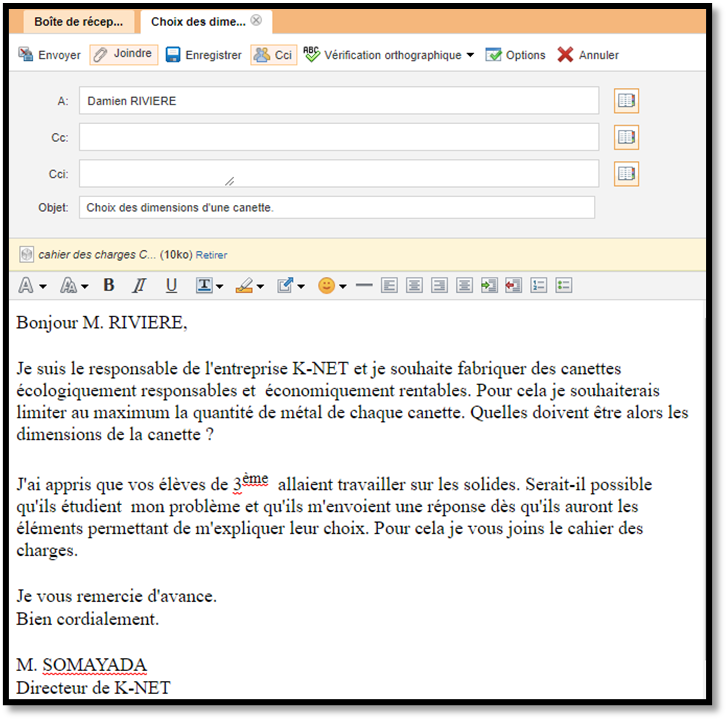 | 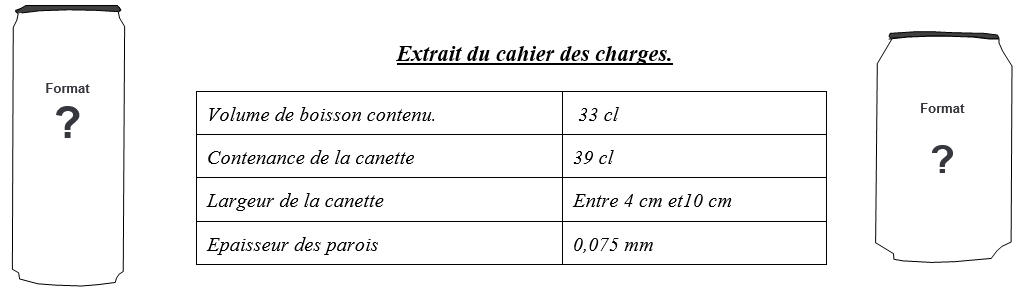 |
Déroulement de l'activité
Les élèves lisent l’énoncé, puis après un temps de réflexion individuelle, ils commencent à élaborer une stratégie de résolution du problème par groupe de 4.
La modélisation du problème
Une première modélisation évidente !
Les élèves vont tous, très naturellement, modéliser la canette par un cylindre et vont considérer comme négligeable les rebords, les creux… Quand je leur demande pourquoi, voici les réponses que j’obtiens : « c’est évident ! », « qu’est-ce que vous voulez qu’on prenne d’autre ? » …
Une deuxième modélisation qui pose plus de difficultés !
Les élèves ont beaucoup plus de difficultés à savoir ce qu’ils doivent calculer et à trouver le lien entre les différentes grandeurs : « Est-ce le volume qu’il faut calculer ? », « Quel rapport entre la quantité de métal et le volume ? » Et certains vont même jusqu’à : « Si elles ont le même volume, elles utilisent forcément la même quantité de métal ».
Tous les groupes demandent s’ils peuvent avoir les 2 formats de canettes pour pouvoir les mesurer et faire des calculs. Voici les premiers résultats obtenus :
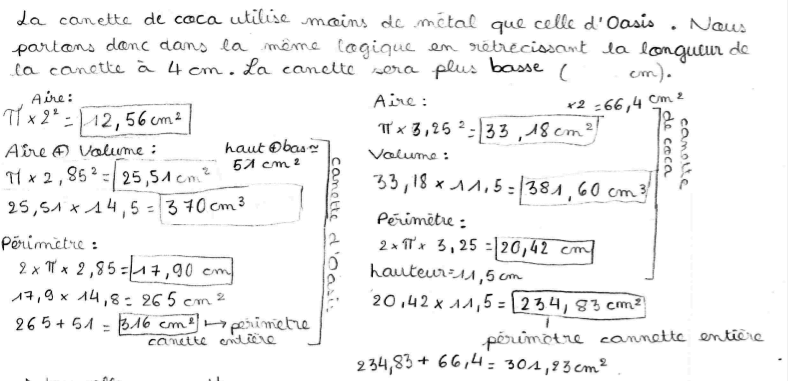 | 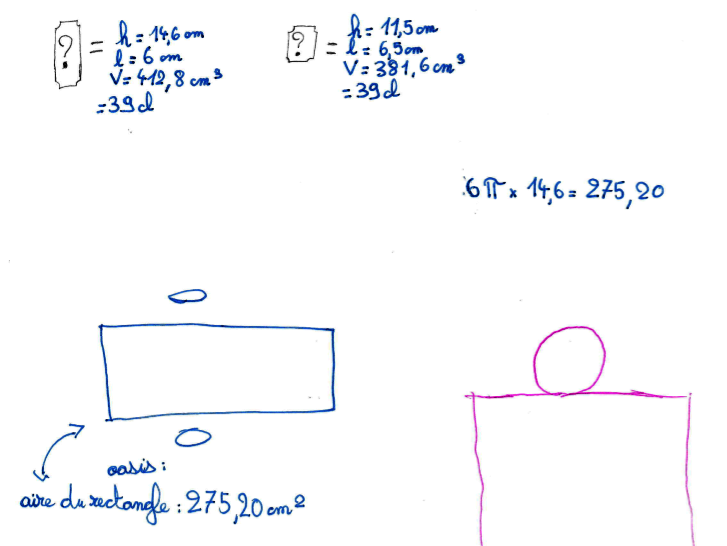 | 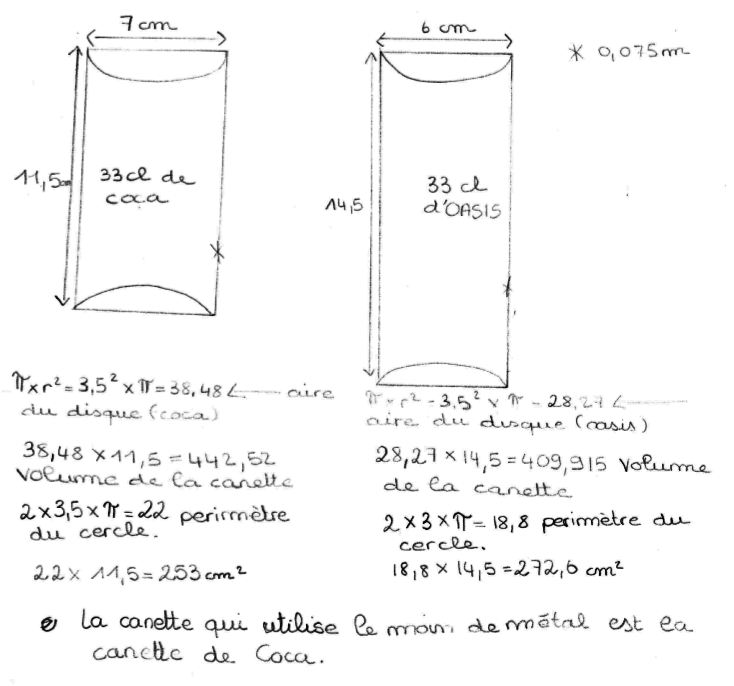 |
| Dans cet exemple, les élèves calculent des grandeurs sans savoir si elles ont un sens réel, notamment le périmètre de la canette. | Dans ce 2ème exemple, les élèves ont compris le lien entre l’aire du patron et la quantité de métal utilisé. | Dans ce 3ème exemple, les élèves réussissent à comparer les 2 canettes fournies. |
Presque tous les élèves, ont fini par réussir à comparer la surface latérale des 2 canettes qu’ils avaient à disposition.
Seuls 3 groupes parmi les 7 sont allés plus loin et ont essayé de généraliser la méthode afin de minimiser la surface latérale.
L'optimisation
Ils ont tous commencé par des essais ; et très rapidement ils ont pris conscience des contraintes du problème : « Si je choisis un rayon et une hauteur au cylindre, je ne suis pas sûr que le volume soit de 39 cl ou 390 cm3. »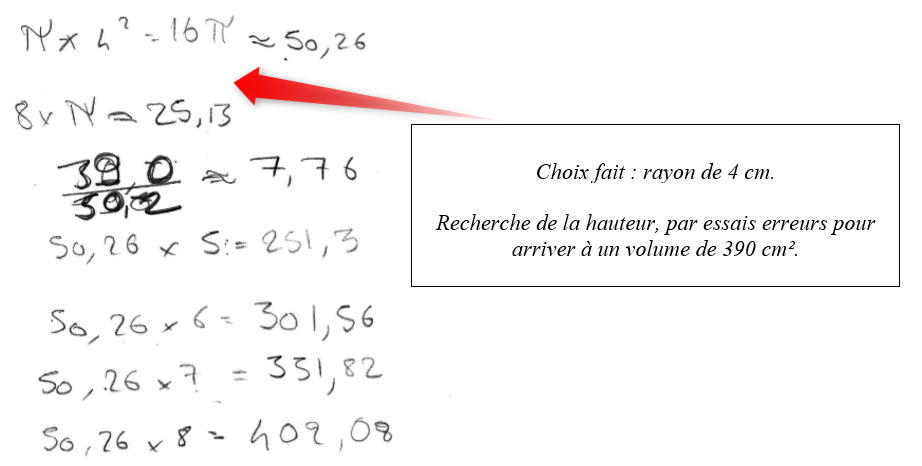
Un groupe résume parfaitement la situation :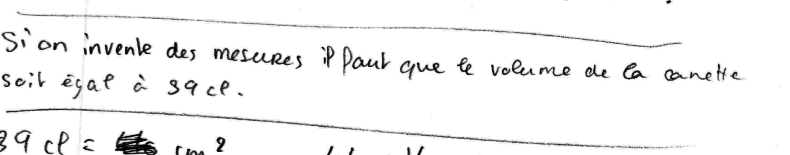 Ce groupe met alors en place un algorithme permettant de trouver la surface latérale du cylindre quand la hauteur est fixée.
Ce groupe met alors en place un algorithme permettant de trouver la surface latérale du cylindre quand la hauteur est fixée.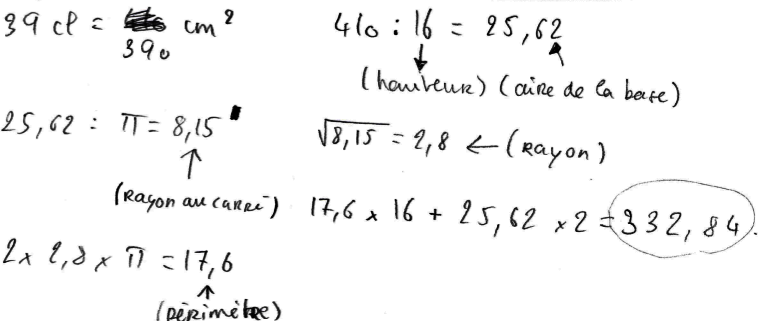

Un groupe résume parfaitement la situation :
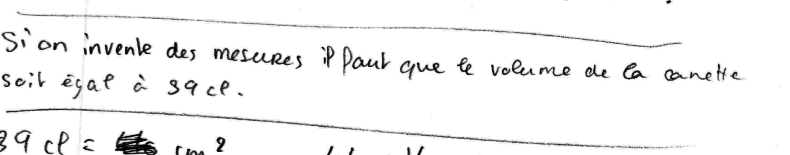
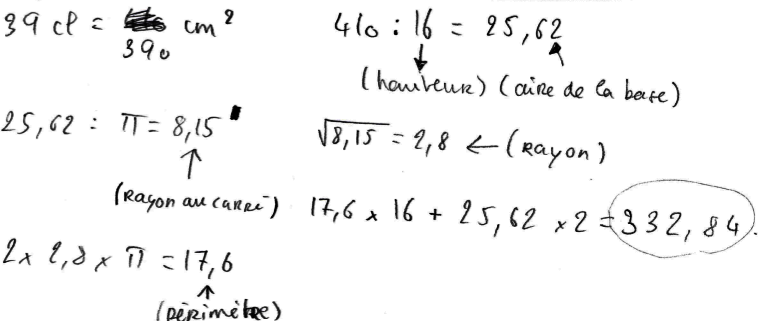
La modélisation informatique
2 groupes décident d’utiliser le tableur pour faire plus d’essais.
Les 2 stratégies sont différentes :
Les 2 stratégies sont différentes :
| Le premier groupe fixe la hauteur | Le deuxième groupe fixe le rayon |
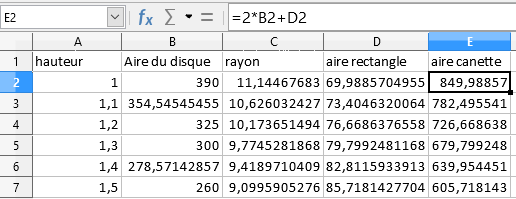 ...  | 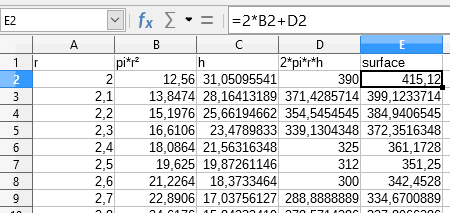 ...  |
Pour finir : le lien avec les fonctions
Quand j’ai ramassé la synthèse, voilà ce que j’ai découvert au dos d’une feuille :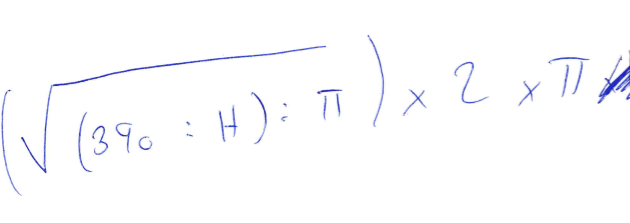
Lors de la synthèse de l’activité un lien entre la formule trouvée, et le tableur que l’on peut apparenter à un tableau de valeur et la notion de fonction a été mis en évidence. Certains élèves ont alors fait remarquer fort justement que l’on aurait pu faire un graphique. Après étude du tableur, les élèves sont arrivés à l’idée que le graphique ne serait pas plus précis.
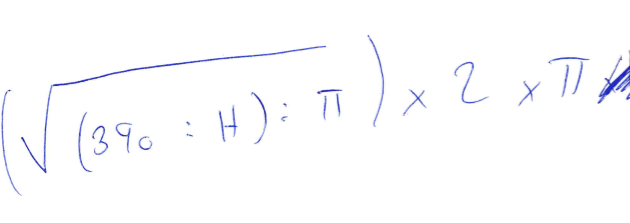
Lors de la synthèse de l’activité un lien entre la formule trouvée, et le tableur que l’on peut apparenter à un tableau de valeur et la notion de fonction a été mis en évidence. Certains élèves ont alors fait remarquer fort justement que l’on aurait pu faire un graphique. Après étude du tableur, les élèves sont arrivés à l’idée que le graphique ne serait pas plus précis.
Damien Rivière, Enseignant au collège Pierre Dubois - Laval (53)
information(s) pédagogique(s)
niveau : tous niveaux, Cycle 4, 3ème
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

