espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
se garer à Nantes
mis à jour le 03/06/2020
Pourquoi ne pas utiliser certaines données brutes, issues d’un « open data », afin de proposer un problème à modéliser.
mots clés : modélisation, statistique à deux variables
Origine du problème - recherche de l’information
L’objectif est d’utiliser certaines données brutes issues d’un « open data » afin de proposer un problème à modéliser.
Sur le site « Éduscol », on a des informations sur les données ouvertes :
Une donnée ouverte (en anglais open data) est une information publique brute, qui a vocation à être librement accessible et réutilisable. La philosophie pratique des données ouvertes préconise une libre disponibilité, pour tous et chacun, sans restriction de copyright, brevets ou d'autres mécanismes de contrôle.
Les données du problème ont été trouvées sur le site data.Nantesmetropole.fr.
Contexte
Classe concernée : classe de terminale STMG – classe de terminale technologique – maths complémentaires voie générale.
Durée de la séquence : 1,5 heure de recherche, de mise au point et de bilan en deux séances. Les élèves avaient des ordinateurs à disposition.
Objectifs : ce problème est proposé juste avant les vacances de février, environ deux semaines après la fin d’une séquence autour des statistiques à deux variables – entre autres les représentations graphiques (nuage de points – point moyen), ainsi que le travail portant sur l’approximation affine par la méthode des moindres carrés. L’un des objectifs est de constater si les élèves ont retenu les moments où on peut utiliser un ajustement affine.
Depuis le début d’année, les élèves ont aussi beaucoup travaillé autour du taux moyen.
Les suites ont été vues en première, notamment les suites particulières arithmétiques et géométriques. Le travail sur les suites en terminale n’est pas encore finalisé.
Durée de la séquence : 1,5 heure de recherche, de mise au point et de bilan en deux séances. Les élèves avaient des ordinateurs à disposition.
Objectifs : ce problème est proposé juste avant les vacances de février, environ deux semaines après la fin d’une séquence autour des statistiques à deux variables – entre autres les représentations graphiques (nuage de points – point moyen), ainsi que le travail portant sur l’approximation affine par la méthode des moindres carrés. L’un des objectifs est de constater si les élèves ont retenu les moments où on peut utiliser un ajustement affine.
Depuis le début d’année, les élèves ont aussi beaucoup travaillé autour du taux moyen.
Les suites ont été vues en première, notamment les suites particulières arithmétiques et géométriques. Le travail sur les suites en terminale n’est pas encore finalisé.
Le problème
Les élèves se voient distribuer une feuille avec les informations données par l’open data.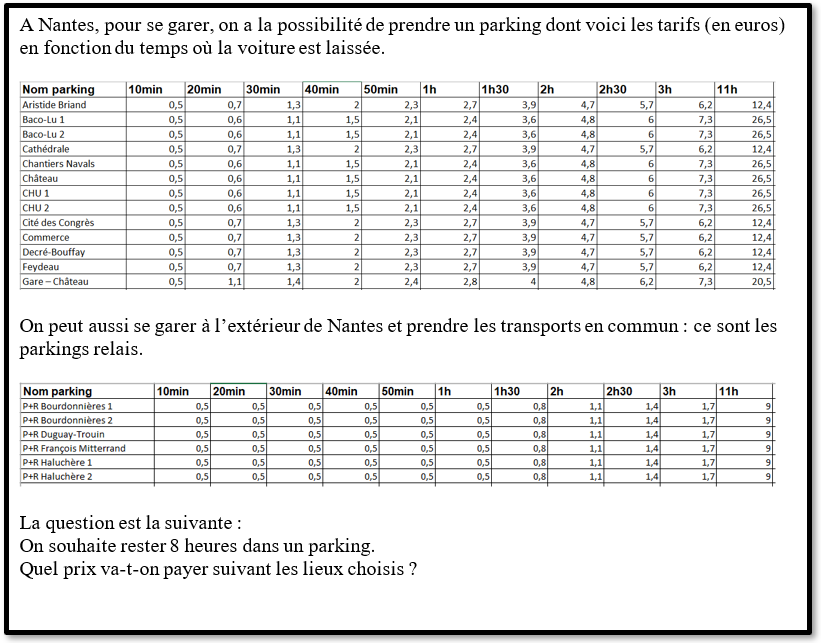

Les modèles possibles
Rappel des compétences à développer :
les élèves ont plusieurs choix possibles pour cette modélisation en lien avec leur programme.
les élèves ont plusieurs choix possibles pour cette modélisation en lien avec leur programme.
- Utilisation du taux moyen.
- Utilisation d’un ajustement affine.
- Traduire le problème à l’aide d’un nuage de points.
- Elaborer une simulation numérique (tableur).
Déroulement de l’activité
L’activité en elle-même s’est déroulée en 3 parties.
1) Prise de connaissances du problème (15 minutes)
Les élèves prennent connaissance des deux tableaux et sont un peu « impressionnés » par le nombre de calcul à effectuer. Rapidement, certains émettent l’idée d’un tableau de proportionnalité, ce qui semblerait logique.
Très vite cependant, des élèves remarquent qu’il n’y a pas de proportionnalité : pour certains parkings, le doublement du temps ne correspond pas au doublement du prix.
D’autres remarquent que les tarifs peuvent se regrouper. Je leur indique qu’il s’agit en fait de distinguer les parkings « souterrain », des parkings extérieurs type « enclos ».
Un premier bilan sur ces réponses (notamment le tri des données) est effectué et différentes pistes de travail sont établies. Les groupes sont mis en place pour proposer des réponses plus complètes et élaborées.
| Modéliser |
|
2) Elaboration de réponses
Les élèves se répartissent en groupe de 3 ou 4 et commencent à chercher l’interpolation.
Une piste est souvent entendue mais abandonnée par tous : plusieurs groupes ont en effet l’idée d’utiliser le taux moyen mais les calculs n’aboutissent pas.
La piste privilégiée : tous les groupes souhaitent visualiser la situation avec un graphique. Il s’agit d’une modélisation à l’aide d’une représentation graphique prémices à l’exploitation de fonctions. Dans de nombreux groupes le problème principal est le suivant : comment combiner les minutes et les heures ? Faut-il faire deux représentations graphiques (ce qu’a fait effectivement un groupe).
Une représentation graphique « acceptable » (si on excepte l’absence de titre et d’indication d’unités sur les axes).
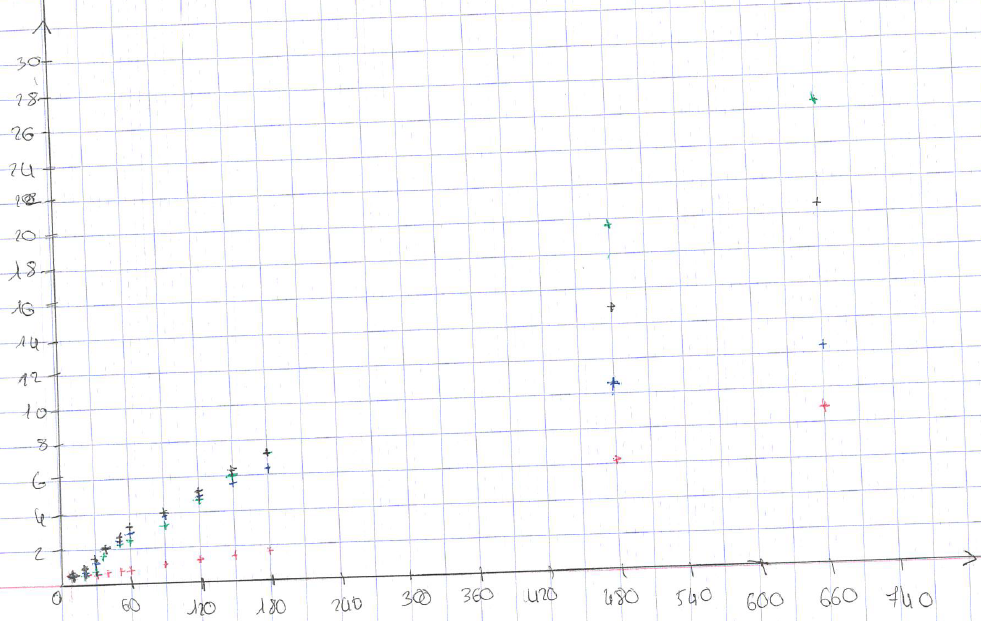
Un autre groupe propose deux nuages de points différents :
Pour les minutes :
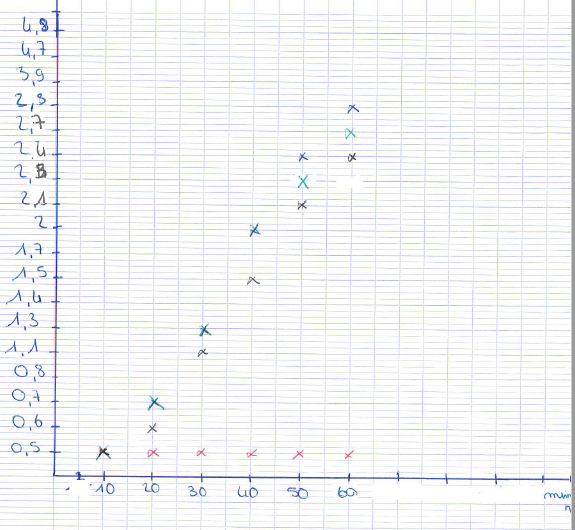
Pour les heures (avec problème pour placer 11h…). Ce choix peut se justifier car parfois la proportionnalité est établie. Par exemple pour les parkings « Baco 1&2 » entre 1h et 3h.
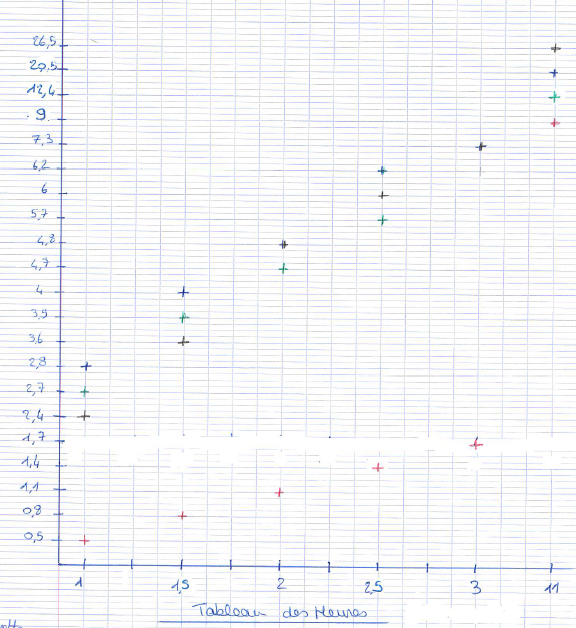
On peut remarquer que pour tous les groupes :
- Ils ne vont pas s’en servir pour « justifier » l’emploi ou non d’un ajustement affine.
- Seulement 2 groupes vont utiliser spontanément les ordinateurs et le tableur. Il s’agit donc d’élaborer une simulation numérique et utiliser un tableur.
Les groupes souhaitent maintenant trouver une réponse plus précise à partir du nuage de points donnés, il modélise la situation à l’aide d’un outil statistique : un ajustement par la méthode des moindres carrés.
L’ajustement affine tient compte le plus souvent de tous les points :
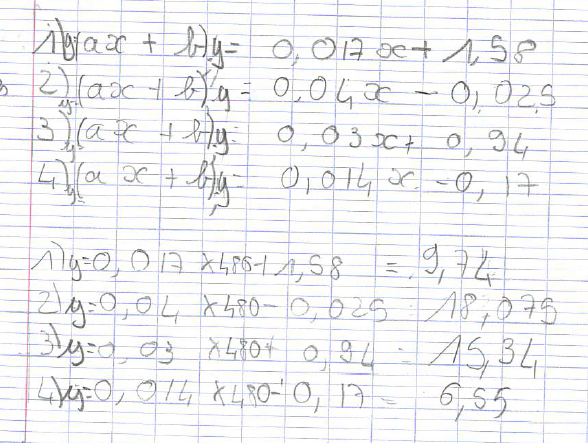
3) Bilan et perspectives
Le bilan reprend les différentes méthodes utilisées. Je soulève néanmoins quelques questions :
- Pourquoi n’ont-ils pas « poussé » la méthode utilisant un taux moyen (progression géométrique) ?
- Un autre modèle donnerait une autre réponse. Quelle est la meilleure ?
Le bilan va donc porter sur la validité des choix effectués, notamment comment valider ou invalider un modèle. Le cas des parkings relais va être particulièrement étudié lors de ce bilan – le nuage de points ne permettant pas de « supposer » un ajustement affine.
Conclusion
L’utilisation des « données ouvertes » a permis de construire un problème « simple » qui a intéressé globalement les élèves. A juste titre néanmoins, un élève m’a fait remarquer qu’il n’allait pas s’amuser à calculer le prix au bout de 8heures de cette façon. Au final, c’est la validité du modèle qui était importante : peut-on remettre en cause un modèle, notamment si le professeur de mathématiques l’exploite ? Oui, on peut...
Fabrice Foucher, enseignant au lycée Jacques Prévert - Savenay (44)
information(s) pédagogique(s)
niveau : tous niveaux, Terminale STG
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA


