espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
un terrain à aménager
mis à jour le 03/06/2020
mots clés : modélisation, équation second degré
Contexte
Classes concernées : classes de seconde – groupes de première.
Il s’agit de problèmes aboutissant à des situations du second degré. On peut travailler au choix :
La question posée aux élèves peut être adaptée en fonction du niveau et de l’avancement du programme.
Il s’agit de problèmes aboutissant à des situations du second degré. On peut travailler au choix :
- Equations du second degré.
- Optimisation et second degré.
- Différentes formes possibles pour répondre à un problème.
La question posée aux élèves peut être adaptée en fonction du niveau et de l’avancement du programme.
L’énoncé du problème
Le problème de départ a été adapté de problèmes classiques vus dans différents manuels. Ces problèmes sont regroupés à partir du plan d’une parcelle qu’on obtient dès qu’on achète un domicile. Le plan proposé est donc « bien réel » et les recherches des informations sont importantes pour démarrer la résolution. La situation aboutit notamment à des dimensions de terrain moins « classiques » pour les élèves : 11 mètres par 10.17 mètres.
Déroulé de la séance : modéliser est un prétexte ?
Les élèves ont quelques difficultés à bien analyser le problème. Si les situations présentées ensuite sont assez classiques, il est nécessaire de trouver les bonnes dimensions du terrain.
Il faut donc apprendre à lire un plan, et déduire les bonnes dimensions. Si en réalité, les parcelles sont rarement des rectangles « parfaits » (c’est-à-dire vérifiant toutes les propriétés d’un rectangle), des choix doivent être effectués pour simplifier les calculs (entre autres l’aire d’un rectangle).
Rapidement, un premier bilan est effectué pour préciser ces résultats intermédiaires afin d’acter les dimensions et donc d’acter un modèle unique. On peut faire remarquer (parfois un élève s’en charge) que c’est peut-être ici qu’intervient la seule véritable modélisation : un professionnel assimilerait bien ce jardin à un rectangle – pas certain néanmoins ensuite qu’il propose des situations aussi « pauvres » esthétiquement.
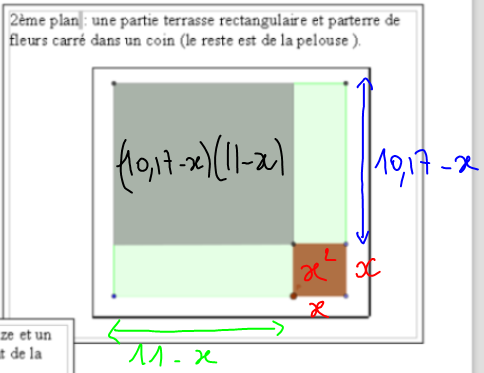
Les 3 aménagements proposés sont ensuite travaillés dans chaque groupe. Une simulation informatique est projetée pour bien comprendre les variations des différentes demandes (terrasse, pelouse et parterre). La modélisation (dans le sens « traduire en langage mathématiques une situation réelle) peut consister ici à introduire une variable. Suivant le choix effectué de cette variable, les résolutions seront plus ou moins complexes.
L’enseignant peut passer dans chaque groupe pour finaliser (ou non) le choix effectué et indiquer le plan à traiter. Il est possible de différencier le travail suivant la nature des groupes de différentes façons :
Il faut donc apprendre à lire un plan, et déduire les bonnes dimensions. Si en réalité, les parcelles sont rarement des rectangles « parfaits » (c’est-à-dire vérifiant toutes les propriétés d’un rectangle), des choix doivent être effectués pour simplifier les calculs (entre autres l’aire d’un rectangle).
Rapidement, un premier bilan est effectué pour préciser ces résultats intermédiaires afin d’acter les dimensions et donc d’acter un modèle unique. On peut faire remarquer (parfois un élève s’en charge) que c’est peut-être ici qu’intervient la seule véritable modélisation : un professionnel assimilerait bien ce jardin à un rectangle – pas certain néanmoins ensuite qu’il propose des situations aussi « pauvres » esthétiquement.
Les 3 aménagements proposés sont ensuite travaillés dans chaque groupe. Une simulation informatique est projetée pour bien comprendre les variations des différentes demandes (terrasse, pelouse et parterre). La modélisation (dans le sens « traduire en langage mathématiques une situation réelle) peut consister ici à introduire une variable. Suivant le choix effectué de cette variable, les résolutions seront plus ou moins complexes.
L’enseignant peut passer dans chaque groupe pour finaliser (ou non) le choix effectué et indiquer le plan à traiter. Il est possible de différencier le travail suivant la nature des groupes de différentes façons :
- 1 groupe travaille sur un plan spécifique.
- Chaque membre du groupe s’occupe d’un plan.
Bilan
Des choix doivent être faits pour la synthèse. Tous les cas ne sont pas traités. Il s’agit par contre de mettre en avant les points communs.
En cela, l’utilisation d’une échelle descriptive peut aider pour faire comprendre aux élèves les différentes démarches que ce soit pour la compétence « Chercher » mais aussi pour la compétence « Modéliser ». Il est d’ailleurs difficile de différencier les deux : l’un n’allant pas sans l’autre dans ce type de problème.
Une fois les équations trouvées, la résolution proprement dite fait appel à d’autres compétences. Il peut s’agir de représenter les courbes des fonctions associées à ces équations et de répondre à la question posée ou de mettre en œuvre la compétence calculer pour une résolution précise de ces équations.
Un retour au problème initial fait partie de la modélisation mais ne me semble pas être une « contrainte importante » dans ce type de problème dans le sens où il ne s’agit pas d’invalider un modèle.
 |  |
En cela, l’utilisation d’une échelle descriptive peut aider pour faire comprendre aux élèves les différentes démarches que ce soit pour la compétence « Chercher » mais aussi pour la compétence « Modéliser ». Il est d’ailleurs difficile de différencier les deux : l’un n’allant pas sans l’autre dans ce type de problème.
Une fois les équations trouvées, la résolution proprement dite fait appel à d’autres compétences. Il peut s’agir de représenter les courbes des fonctions associées à ces équations et de répondre à la question posée ou de mettre en œuvre la compétence calculer pour une résolution précise de ces équations.
Un retour au problème initial fait partie de la modélisation mais ne me semble pas être une « contrainte importante » dans ce type de problème dans le sens où il ne s’agit pas d’invalider un modèle.
Fabrice Foucher, enseignant au lycée Jacques Prévert - Savenay (44)
information(s) pédagogique(s)
niveau : tous niveaux, 2nde
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA



