espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
la course aux dés
mis à jour le 20/05/2021
mots clés : probabilité, modélisation
Règles inspirées du jeu de société « Rallyman »
 On utilise une piste avec des cases et des pions pour marquer la position du joueur. A chaque tour, le joueur peut avancer son pion d’autant de cases qu’il veut (maximum 5) en respectant les règles suivantes :
On utilise une piste avec des cases et des pions pour marquer la position du joueur. A chaque tour, le joueur peut avancer son pion d’autant de cases qu’il veut (maximum 5) en respectant les règles suivantes :
Est-ce qu’il est risqué de foncer ?
En classe : Sans posséder le jeu, il peut être reproduit à l’aide de dés à 6 faces de deux couleurs (1 bleu pour ceux avec un panneau et 4 rouges pour ceux à deux panneaux). Par convention, le 1 sur un dé bleu et les 1 et 2 sur un dé rouge correspondent au panneau attention.
 On utilise une piste avec des cases et des pions pour marquer la position du joueur. A chaque tour, le joueur peut avancer son pion d’autant de cases qu’il veut (maximum 5) en respectant les règles suivantes :
On utilise une piste avec des cases et des pions pour marquer la position du joueur. A chaque tour, le joueur peut avancer son pion d’autant de cases qu’il veut (maximum 5) en respectant les règles suivantes :- Il faut lancer un dé pour chaque case parcourue
- Chaque dé ne peut être lancer qu’une seule fois durant un tour. Il y a 1 dé bleu avec une face marquée d’un panneau « attention » et quatre dés rouges avec deux faces marquées d’un panneau « attention ».
- Si lors d’un même tour, le joueur obtient trois panneaux « attention », c’est la chute et le joueur est éliminé de la partie
- En assurant, il les lance un par un et peut donc s’arrêter avant de risquer la chute
- En fonçant, il les lance tous d’un seul coup mais reçoit un jeton bonus qui lui servira à annuler un « attention » sur un coup « en assurant » plus tard dans la partie.
Est-ce qu’il est risqué de foncer ?
En classe : Sans posséder le jeu, il peut être reproduit à l’aide de dés à 6 faces de deux couleurs (1 bleu pour ceux avec un panneau et 4 rouges pour ceux à deux panneaux). Par convention, le 1 sur un dé bleu et les 1 et 2 sur un dé rouge correspondent au panneau attention.
Objectif
L’idée est de partir des règles d’un jeu et de modéliser la situation pour prendre une décision éclairée en jouant.
Plusieurs approches sont possibles. Les élèves majoritairement s’engagent vers la représentation par un arbre qui peut s’avérer dense s’ils utilisent les 7 dés possibles. La simulation est aussi une direction étudiée à travers la création d’un tableur ou d’un programme en Python.
La modélisation choisie par les élèves efface l’aspect simultané du lancer des dés au profit d’une chronologie. La combinatoire présente dans ce jeu peut aussi être traitée dans le cadre de l’enseignement de spécialité en Terminale Générale
Pour conclure, je leur ai proposé une approche à travers les variables aléatoires qui donne des résultats moins précis mais facilement calculables et qui n’introduisent pas cet ordre dans les lancers.
Plusieurs approches sont possibles. Les élèves majoritairement s’engagent vers la représentation par un arbre qui peut s’avérer dense s’ils utilisent les 7 dés possibles. La simulation est aussi une direction étudiée à travers la création d’un tableur ou d’un programme en Python.
La modélisation choisie par les élèves efface l’aspect simultané du lancer des dés au profit d’une chronologie. La combinatoire présente dans ce jeu peut aussi être traitée dans le cadre de l’enseignement de spécialité en Terminale Générale
Pour conclure, je leur ai proposé une approche à travers les variables aléatoires qui donne des résultats moins précis mais facilement calculables et qui n’introduisent pas cet ordre dans les lancers.
Travaux d'élèves
Pour débuter certains groupes n’utilisent que 3 dés :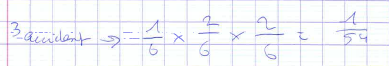
Dans ce cas, il faut que tous les dés indiquent « attention ». C’est le cas le plus facile en termes de combinatoire, mais il est utile pour débuter un raisonnement. Le passage à 4 dés pose alors un problème puisqu’il suffit d’avoir 3 « attentions » sur les 4 dés. Il faut donc considérer les différents cas possibles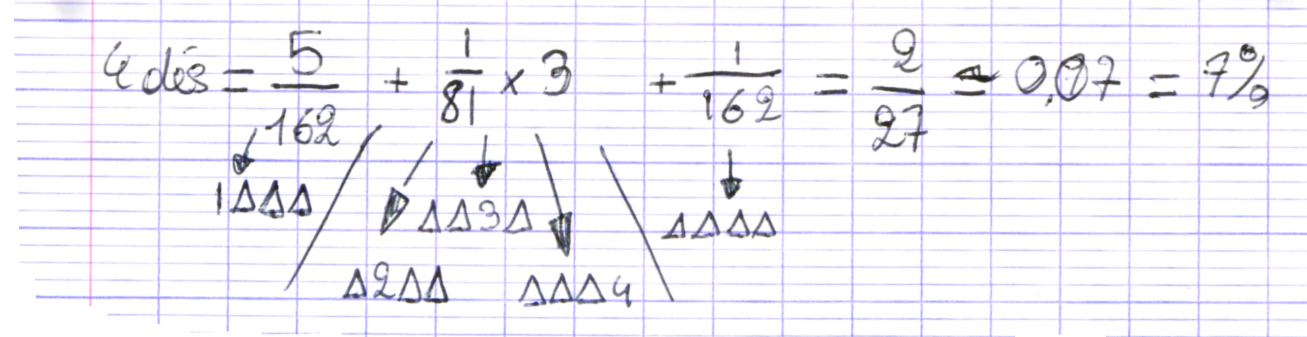
Pour comprendre les possibilités, les élèves représentent la situation à travers un arbre :
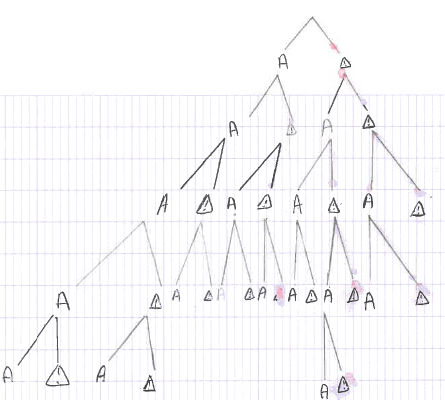
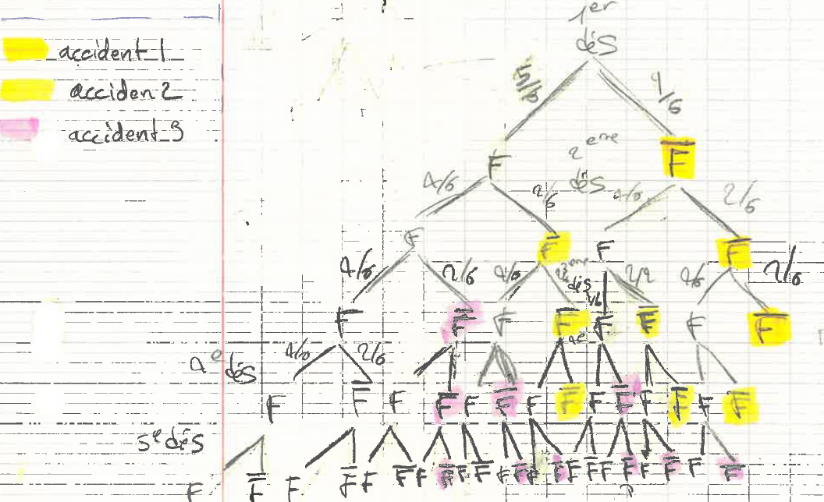
Ici sur les deux exemples les cinq dés sont utilisés. Dans le deuxième, on peut voir les probabilités notées sur chaque branche.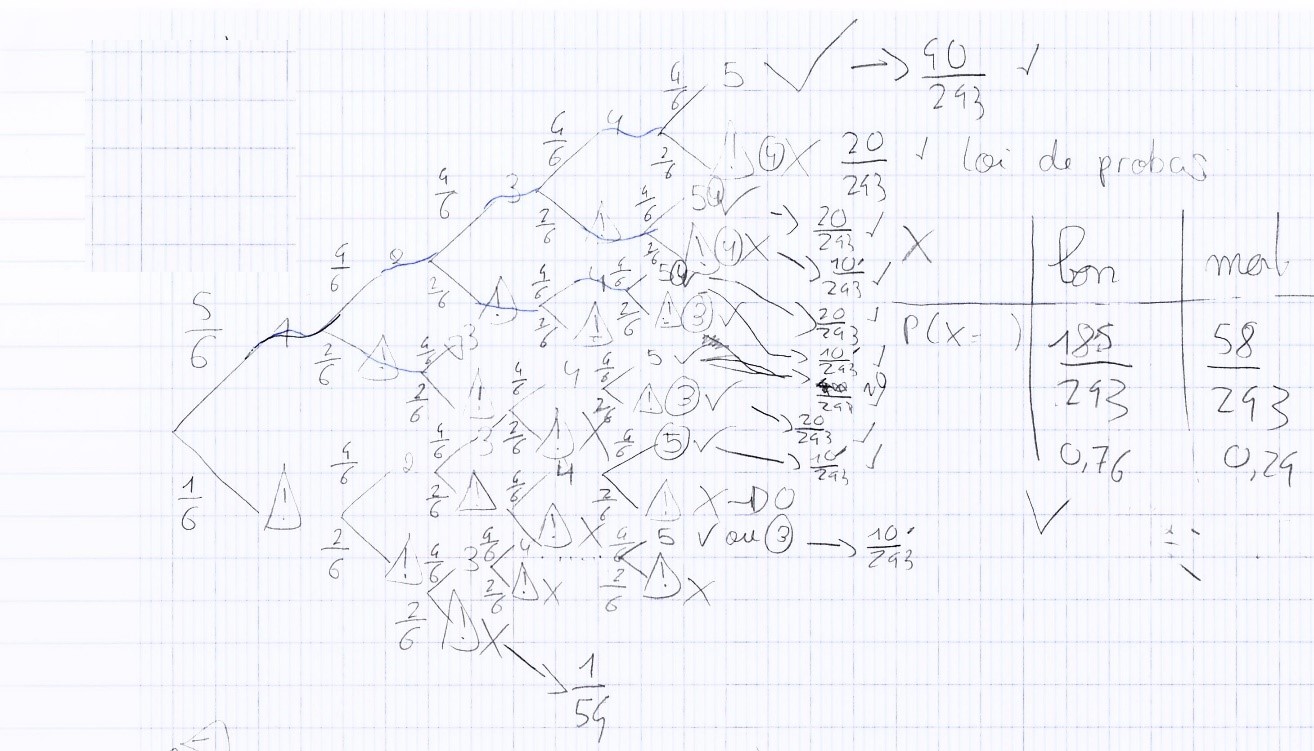
L’arbre peut être exploité pour obtenir la probabilité d’avoir une chute sur un lancer de 5 dés. Celle-ci est de 58/243 soit environ 24% d’après ce groupe d’élève. Le résultat est ici faux tous les cas de non chute ne sont pas comptabilisés.
L’un des groupes a produit un fichier sur tableur qui confirme les résultats trouvés :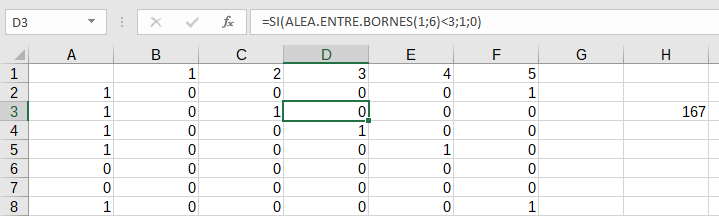
Les colonnes B à F représentent les dés et indiquent 1 lorsque le panneau « attention » est obtenu. La colonne A fait la somme des autres colonnes et indique donc s’il y a un accident sur un tirage.
 Ici 1000 tirages sont effectués soit sur 5 dés environ 17% de chance d’accident.
Ici 1000 tirages sont effectués soit sur 5 dés environ 17% de chance d’accident.
Si X est la variable aléatoire pour le nombre de panneau attention sur un dé et Y correspond à celle pour deux panneaux alors ses deux variables suivent des lois de Bernoulli. Chaque dé peut être modélisé par une de ses deux variables et les dés sont indépendants. On peut rappeler ici que si l’indépendance est vérifiée alors E(X+Y)=E(X)+E(Y).
D’après les résultats sur la loi de Bernoulli, E(X)=1/6 et E(Y)=2/6.
Ainsi en lançant les 5 dés noirs (soit 1 dé type X et 4 types Y), on obtient en moyenne :
1/6 + 4 × 2/6 = 9/6 = 1,5 panneaux.
Il y a donc peu de risque d’accident puisqu’on est loin de 3.
En exploitant la loi binomiale, on peut trouver les valeurs exactes. On note A la variable aléatoire correspondant au nombre de panneaux « attention » obtenus.
On remarque d’abord que P(« Chute)= 1 – P(A=0) – P(A=1) – P(A=2), et on peut calculer ces trois probabilités :
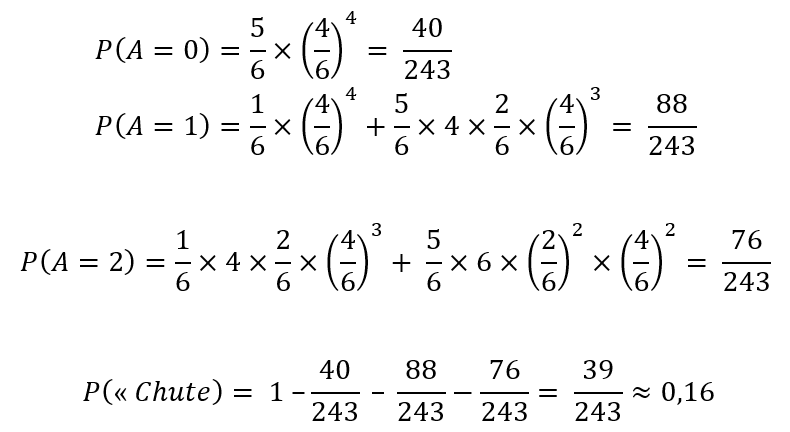
La probabilité d’une chute en lançant les cinq dés est d’environ 16% ce qui correspond à la simulation.
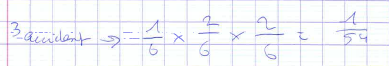
Dans ce cas, il faut que tous les dés indiquent « attention ». C’est le cas le plus facile en termes de combinatoire, mais il est utile pour débuter un raisonnement. Le passage à 4 dés pose alors un problème puisqu’il suffit d’avoir 3 « attentions » sur les 4 dés. Il faut donc considérer les différents cas possibles

Pour comprendre les possibilités, les élèves représentent la situation à travers un arbre :


Ici sur les deux exemples les cinq dés sont utilisés. Dans le deuxième, on peut voir les probabilités notées sur chaque branche.

L’arbre peut être exploité pour obtenir la probabilité d’avoir une chute sur un lancer de 5 dés. Celle-ci est de 58/243 soit environ 24% d’après ce groupe d’élève. Le résultat est ici faux tous les cas de non chute ne sont pas comptabilisés.
L’un des groupes a produit un fichier sur tableur qui confirme les résultats trouvés :

Les colonnes B à F représentent les dés et indiquent 1 lorsque le panneau « attention » est obtenu. La colonne A fait la somme des autres colonnes et indique donc s’il y a un accident sur un tirage.
 Ici 1000 tirages sont effectués soit sur 5 dés environ 17% de chance d’accident.
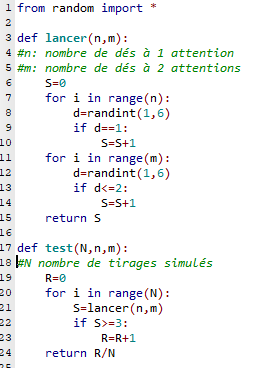
Ici 1000 tirages sont effectués soit sur 5 dés environ 17% de chance d’accident.- L’équivalent peut être fait en Python avec le programme ci-contre :
- A l’aide des variables aléatoires, on peut aborder le problème facilement mais avec des résultats plus faibles.
Si X est la variable aléatoire pour le nombre de panneau attention sur un dé et Y correspond à celle pour deux panneaux alors ses deux variables suivent des lois de Bernoulli. Chaque dé peut être modélisé par une de ses deux variables et les dés sont indépendants. On peut rappeler ici que si l’indépendance est vérifiée alors E(X+Y)=E(X)+E(Y).
D’après les résultats sur la loi de Bernoulli, E(X)=1/6 et E(Y)=2/6.
Ainsi en lançant les 5 dés noirs (soit 1 dé type X et 4 types Y), on obtient en moyenne :
1/6 + 4 × 2/6 = 9/6 = 1,5 panneaux.
Il y a donc peu de risque d’accident puisqu’on est loin de 3.
En exploitant la loi binomiale, on peut trouver les valeurs exactes. On note A la variable aléatoire correspondant au nombre de panneaux « attention » obtenus.
On remarque d’abord que P(« Chute)= 1 – P(A=0) – P(A=1) – P(A=2), et on peut calculer ces trois probabilités :
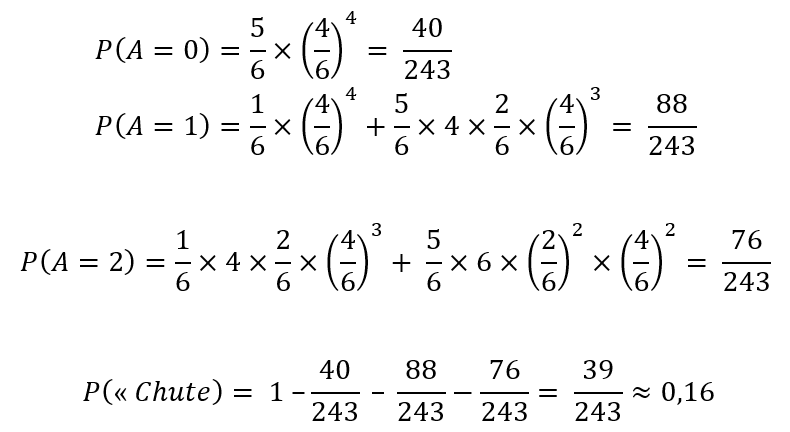
La probabilité d’une chute en lançant les cinq dés est d’environ 16% ce qui correspond à la simulation.
Hervé Diet, enseignant au lycée Touchard Washington, Le Mans (72)
information(s) pédagogique(s)
niveau : tous niveaux
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA



