espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
le lac Berryessa
mis à jour le 25/03/2021
mots clés : modélisation, aire, volume, échelle, pix
Le devoir maison sur le lac de Berryessa a été donné à une classe de 3e. Les élèves ont la possibilité de travailler en binôme. Deux questions font appel à la compétence « modéliser ».
Tout d’abord, le calcul d’une valeur approchée de l’aire
Les stratégies ont été variables mais toutes reposent sur le même principe :

C’est un principe de simplification. Il reste alors à choisir une simplification qui permette d’obtenir une valeur raisonnablement proche de la valeur réelle.
Il a manqué systématiquement un regard sur ce côté « raisonnablement proche », c’est-à-dire un regard critique sur la valeur obtenue par la modélisation choisie.
- Donner et mettre en œuvre une stratégie permettant de déterminer une valeur approchée de l’aire de ce lac.
- Modéliser ce déversoir par un solide que vous décrirez et dont vous calculerez le volume.
Tout d’abord, le calcul d’une valeur approchée de l’aire
Les stratégies ont été variables mais toutes reposent sur le même principe :

C’est un principe de simplification. Il reste alors à choisir une simplification qui permette d’obtenir une valeur raisonnablement proche de la valeur réelle.
Il a manqué systématiquement un regard sur ce côté « raisonnablement proche », c’est-à-dire un regard critique sur la valeur obtenue par la modélisation choisie.
Quelques choix de modélisations
 |  |
Cela a permis de proposer des calculs :

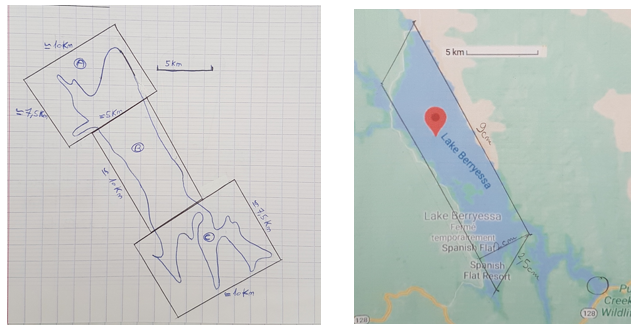
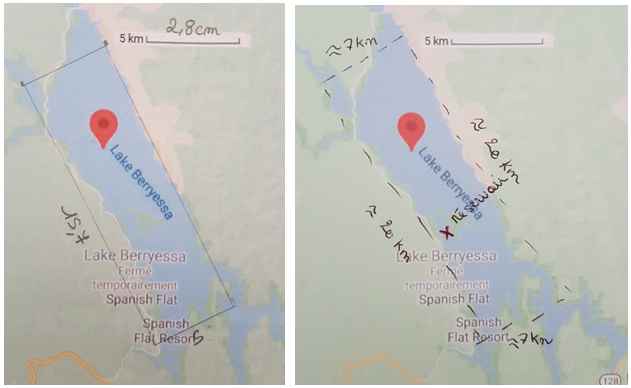
Si on observe des imprécisions de rédaction, on rencontre bien le schéma réel
Un seul élève a proposé une copie numérique, cette possibilité étant offerte.
 « pour donner une estimation de l’Aire du lac il faut prendre l’échelle de graduation de la carte qui est égal à 5km pour 2,5cm, ensuite on va venir faire un rectangle approximatif du lac avec l’échelle graduée. J’ai donc pris les mesures sur la carte et j’estime que le rectangle fait du 4km sur 20km. 4x20=80km² »
« pour donner une estimation de l’Aire du lac il faut prendre l’échelle de graduation de la carte qui est égal à 5km pour 2,5cm, ensuite on va venir faire un rectangle approximatif du lac avec l’échelle graduée. J’ai donc pris les mesures sur la carte et j’estime que le rectangle fait du 4km sur 20km. 4x20=80km² »Ensuite, la modélisation du déversoir
Le texte est plus sibyllin : le mot « entonnoir » par exemple a amené (fort judicieusement d’ailleurs) à des formes un peu compliquées.
Le texte est plus sibyllin : le mot « entonnoir » par exemple a amené (fort judicieusement d’ailleurs) à des formes un peu compliquées.
Quelques choix de modélisations
Le tronc de cône
L'entonnoir
Quelques élèves enfin ont choisi un cylindre, sans que le schéma ne soit présent sur les copies.

Des éléments de correction (voir la fiche complète de l'activité) donnés aux élèves permettent de présenter une autre compétence Pix se rapprochant de « enrichir ses créations majoritairement textuelles ».
 | Compris ici comme une pyramide (ce qui bien sûr n’engendre pas d’impact sur les calculs), la notion de tronc (de cône ou de pyramide) n’est pas maitrisée et l’analyse de la figure est incorrecte. Pour autant, tous les éléments sont là pour que ce regard puisse rapidement évoluer ! |
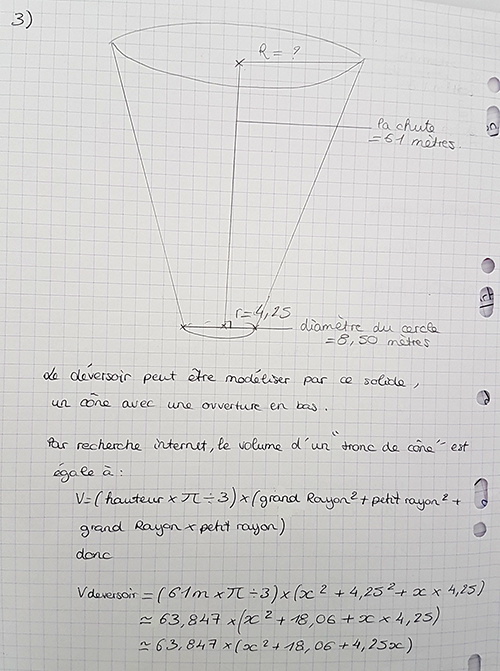 |  Le tronc de cône est visible sur le dessin réalisé. Le tronc de cône est visible sur le dessin réalisé. L’analyse de la figure qui aurait permis d’utiliser un résultat connu a été insuffisante mais compensée par une recherche d’information sur Internet. |
L'entonnoir
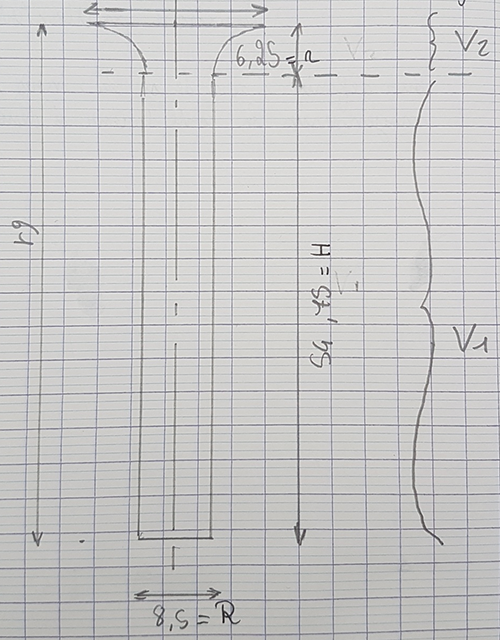 | L’entonnoir est bien décomposé en une partie qui sera assimilée à un cône et une partie cylindrique. Autre version : 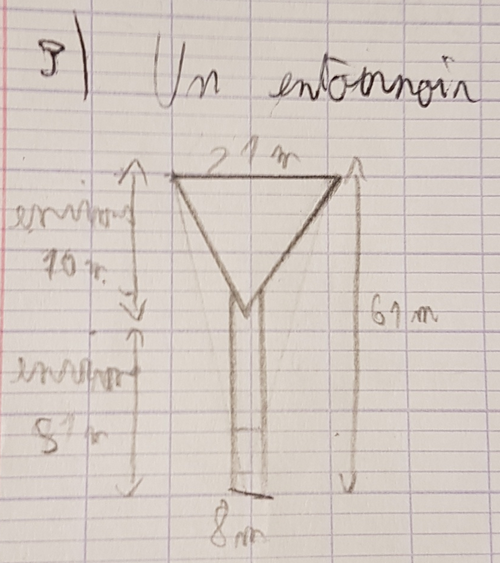 |
Quelques élèves enfin ont choisi un cylindre, sans que le schéma ne soit présent sur les copies.

Des éléments de correction (voir la fiche complète de l'activité) donnés aux élèves permettent de présenter une autre compétence Pix se rapprochant de « enrichir ses créations majoritairement textuelles ».
Yannick Danard, Enseignant au collège Janequin, Avrillé (49)
information(s) pédagogique(s)
niveau : tous niveaux, Cycle 4, 3ème
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

