espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
modéliser et produit scalaire
mis à jour le 30/04/2021
mots clés : produit scalaire, modélisation
Le problème
Il est donné aux élèves au format papier.
Le problème du halage
 Le halage est un mode de traction terrestre des péniches, des coches d’eau et d'une manière générale des bateaux fluviaux, qui consiste à les faire avancer le long d’une rivière, d’un canal, au moyen d’une corde tirée jadis à force de bras ou par des chevaux, à présent par un engin automoteur. Source wikipedia
Le halage est un mode de traction terrestre des péniches, des coches d’eau et d'une manière générale des bateaux fluviaux, qui consiste à les faire avancer le long d’une rivière, d’un canal, au moyen d’une corde tirée jadis à force de bras ou par des chevaux, à présent par un engin automoteur. Source wikipedia
Une longueur de corde étant donnée, expliquer comment doivent être positionnés des chevaux sur la rive par rapport au bateau tracté pour que la traction soit la plus efficace ?
Il s’agit d’un problème d’apparence très classique autour du produit scalaire et qui est utilisé en physique pour mettre en avant le travail d’une force. Néanmoins, d’une part tous les élèves ne suivent pas la spécialité Physique Chimie, d’autre part, bien que présent dans le programme de physique dans le thème « Aspects énergétiques des phénomènes mécaniques », aucun élève qui suit cette spécialité ne l’a encore abordé.
Le problème du halage
 Le halage est un mode de traction terrestre des péniches, des coches d’eau et d'une manière générale des bateaux fluviaux, qui consiste à les faire avancer le long d’une rivière, d’un canal, au moyen d’une corde tirée jadis à force de bras ou par des chevaux, à présent par un engin automoteur. Source wikipedia
Le halage est un mode de traction terrestre des péniches, des coches d’eau et d'une manière générale des bateaux fluviaux, qui consiste à les faire avancer le long d’une rivière, d’un canal, au moyen d’une corde tirée jadis à force de bras ou par des chevaux, à présent par un engin automoteur. Source wikipediaUne longueur de corde étant donnée, expliquer comment doivent être positionnés des chevaux sur la rive par rapport au bateau tracté pour que la traction soit la plus efficace ?
Il s’agit d’un problème d’apparence très classique autour du produit scalaire et qui est utilisé en physique pour mettre en avant le travail d’une force. Néanmoins, d’une part tous les élèves ne suivent pas la spécialité Physique Chimie, d’autre part, bien que présent dans le programme de physique dans le thème « Aspects énergétiques des phénomènes mécaniques », aucun élève qui suit cette spécialité ne l’a encore abordé.
Les interrogations des élèves
Après une recherche individuelle, quelques questions apparaissent autour de la compréhension du problème. Que signifie « une longueur de corde étant donnée » ? La discussion autour de cette longueur ne dure que peu de temps. Il est proposé soit de fixer une longueur (100 mètres) soit de donner une valeur l (en mètres). Au final, les élèves ne comprennent pas bien quels calculs effectuer. Je leur fais remarquer qu’il n’est pas demandé, à priori, d’effectuer des calculs mais d’expliquer la position des chevaux pour une traction efficace. Il s’agit donc de définir un modèle d’efficacité. Il s’agit alors donner un schéma de la situation. La modélisation se rapproche davantage de la compétence représenter : il faut d’abord comprendre les paramètres en jeu avant de proposer un modèle. Les derniers moments de la séance (environ 10 minutes) servent à mettre en place cette modélisation/représentation.
Remarque : une expérience, notamment dans les voies technologiques, peut être aussi menée à priori en apportant une corde et faire tirer une table pour sentir qu’avec un angle plus ouvert il faut un effort plus important. Cette expérience a été faite en bilan pour cette séance avec les éléments qui étaient disponibles (écharpe – table).
Remarque : une expérience, notamment dans les voies technologiques, peut être aussi menée à priori en apportant une corde et faire tirer une table pour sentir qu’avec un angle plus ouvert il faut un effort plus important. Cette expérience a été faite en bilan pour cette séance avec les éléments qui étaient disponibles (écharpe – table).
Quelques réponses des élèves
Toutes font appel à un schéma que je ramasse en fin de séance. Cela permet de regarder les propositions et de présenter dans un certain ordre les représentations effectuées.
Le premier schéma proposé donne juste la façon de tracter le bateau avec très peu de commentaires.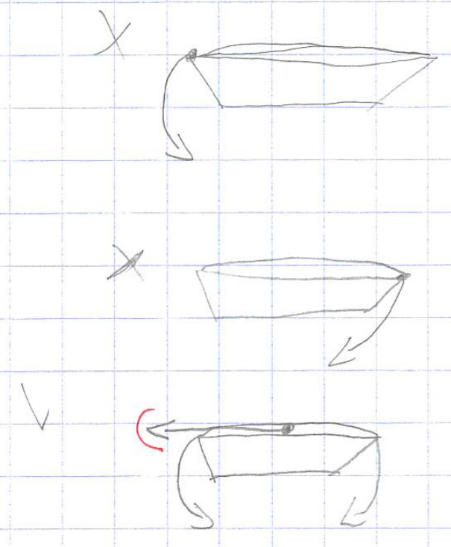 Après explication, les élèves indiquent qu’on ne peut pas le tirer trop sur le côté, ni en arrière mais le plus en avant possible…ce qui est conforme à l’intuition. Néanmoins je leur souligne qu’ils ont tenté d’utiliser (inconsciemment quand même) un outil mathématique bien particulier pour effectuer cette modélisation : le vecteur lié à la géométrie avec sens direction et longueur.
Après explication, les élèves indiquent qu’on ne peut pas le tirer trop sur le côté, ni en arrière mais le plus en avant possible…ce qui est conforme à l’intuition. Néanmoins je leur souligne qu’ils ont tenté d’utiliser (inconsciemment quand même) un outil mathématique bien particulier pour effectuer cette modélisation : le vecteur lié à la géométrie avec sens direction et longueur.
Plusieurs réponses donnent un schéma similaire à celui proposé ci-contre (et retenu ici pour sa vision « aérienne »).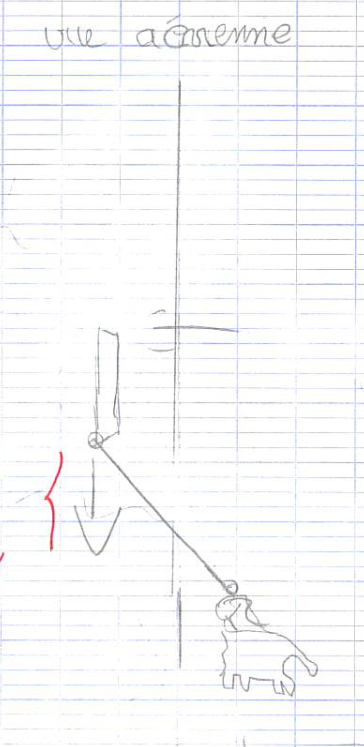 Là encore, le bilan porte sur la tentative d’utilisation d’un vecteur. Ici la traction bien que non encore modélisée par un vecteur est bien présente.
Là encore, le bilan porte sur la tentative d’utilisation d’un vecteur. Ici la traction bien que non encore modélisée par un vecteur est bien présente.
L’importance de l’angle émerge avec la représentation suivante :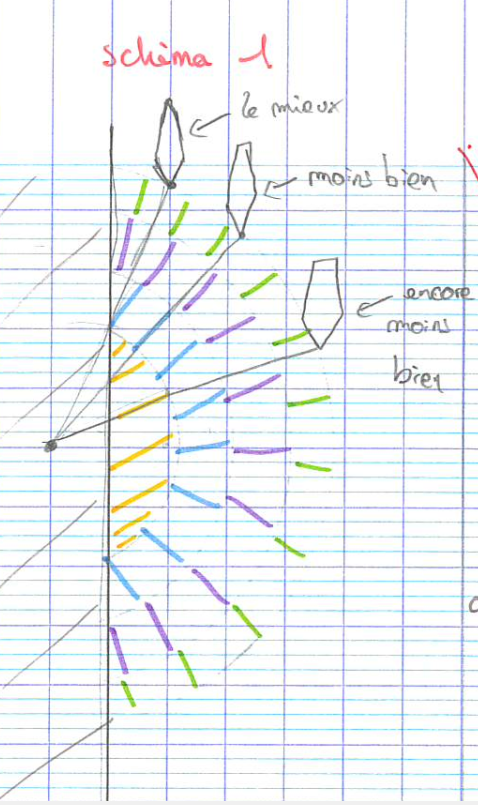
 Les élèves ici mettent en avant qu’un angle aigu proche de 0° permet une traction plus efficace. Une légende est donnée sur le code couleur pour indiquer l’importance apparente de la distance à la rive. Il manque néanmoins une indication claire du sens. Après discussion, les élèves précisent qu’un angle droit ne permet pas de traction. Quant à un angle obtus, cela n’est manifestement pas efficace du tout car la péniche « part » en arrière par rapport à la direction souhaitée.
Les élèves ici mettent en avant qu’un angle aigu proche de 0° permet une traction plus efficace. Une légende est donnée sur le code couleur pour indiquer l’importance apparente de la distance à la rive. Il manque néanmoins une indication claire du sens. Après discussion, les élèves précisent qu’un angle droit ne permet pas de traction. Quant à un angle obtus, cela n’est manifestement pas efficace du tout car la péniche « part » en arrière par rapport à la direction souhaitée.
Cette idée liant l’angle et la longueur de la courbe est reprise avec les explications ci-dessous.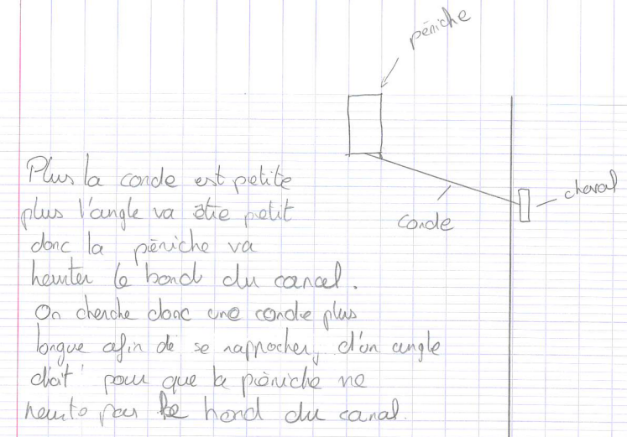
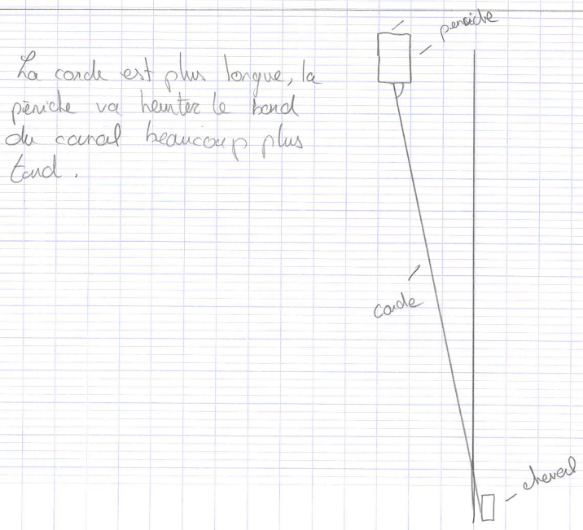
Le premier schéma proposé donne juste la façon de tracter le bateau avec très peu de commentaires.

Plusieurs réponses donnent un schéma similaire à celui proposé ci-contre (et retenu ici pour sa vision « aérienne »).

L’importance de l’angle émerge avec la représentation suivante :


Cette idée liant l’angle et la longueur de la courbe est reprise avec les explications ci-dessous.


Bilan : une modélisation pour quoi faire ?
L’exposé de toutes ces modélisations sous forme de représentation permet de mettre en avant le choix du nouvel outil que je souhaite :
Les élèvent sont maintenant près à la définition du produit scalaire qui sera donnée à savoir celle liant la norme des vecteurs et une mesure de l’angle induit par la position des vecteurs.
La modélisation dans cette activité :
- Un outil où l’angle intervient.
- Un outil représenté à l’aide de vecteurs.
- Un outil où la norme des vecteurs est utile.
Les élèvent sont maintenant près à la définition du produit scalaire qui sera donnée à savoir celle liant la norme des vecteurs et une mesure de l’angle induit par la position des vecteurs.
La modélisation dans cette activité :
- Traduire en langage mathématique une situation réelle de configurations géométriques : il s’agit bien de proposer un schéma simplifiant le problème et permettant de comprendre ce que l’on souhaite.
- Elaborer une simulation géométrique prenant appui sur la modélisation et utilisant un logiciel. Par la suite, je propose en effet une simulation sous Geogebra permettant de comprendre le calcul à effectuer pour déterminer ces premiers produits scalaires.
- Valider ou invalider un modèle. Il ne s’agit pas d’invalider un modèle ici puisque nous n’avons pas de comparaison possible. Cela semble validé un moyen de mesurer l’énergie nécessaire.
Fabrice Foucher, enseignant au lycée Jacques Prévert, Savenay (44)
information(s) pédagogique(s)
niveau : tous niveaux
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

