espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
un drone pour faire des mathématiques
mis à jour le 20/05/2021
Est-il possible de survoler le fort Boyard avec un drone ? Construire des courbes en lien avec le vol d’un drone.
mots clés : courbe, modélisation
[Résumé de l’activité]
Partie 1 : A l’aide de cartes et d’informations sur quatre drones différents, la question est de savoir si l’on peut survoler le fort Boyard à partir de la terre ferme.
Partie 2 : Les élèves ont accès à trois vidéos du vol d’un drone dans un jardin.
Ils doivent construire des courbes représentant :
Et inversement, deux situations différentes peuvent être représentées - modélisées par la même courbe.
Partie 1 : A l’aide de cartes et d’informations sur quatre drones différents, la question est de savoir si l’on peut survoler le fort Boyard à partir de la terre ferme.
Partie 2 : Les élèves ont accès à trois vidéos du vol d’un drone dans un jardin.
Ils doivent construire des courbes représentant :
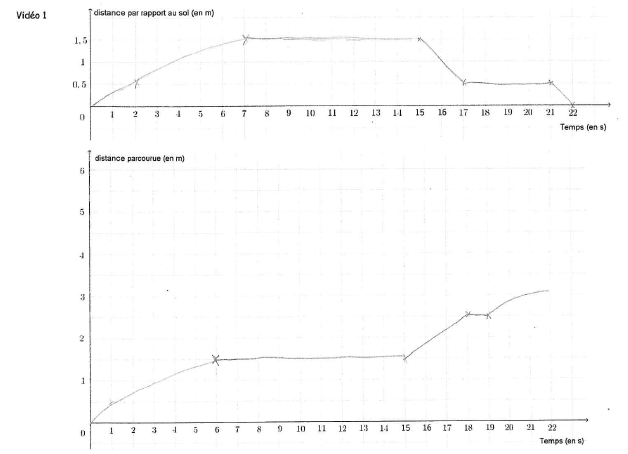
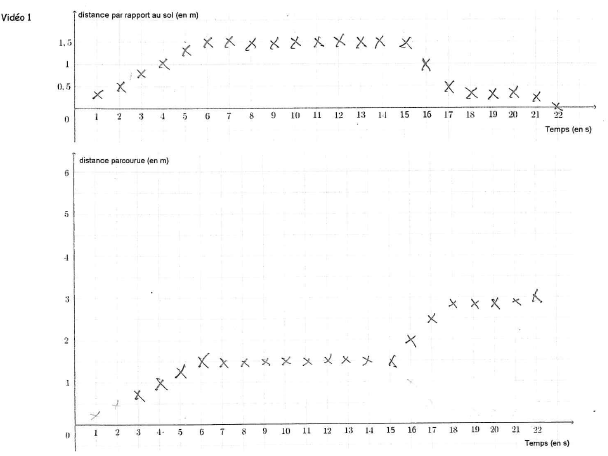
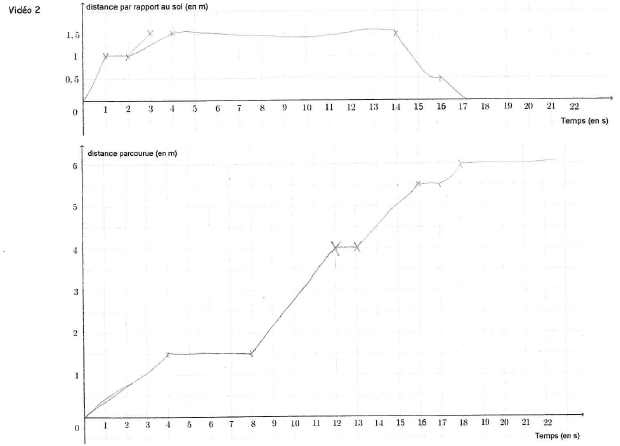
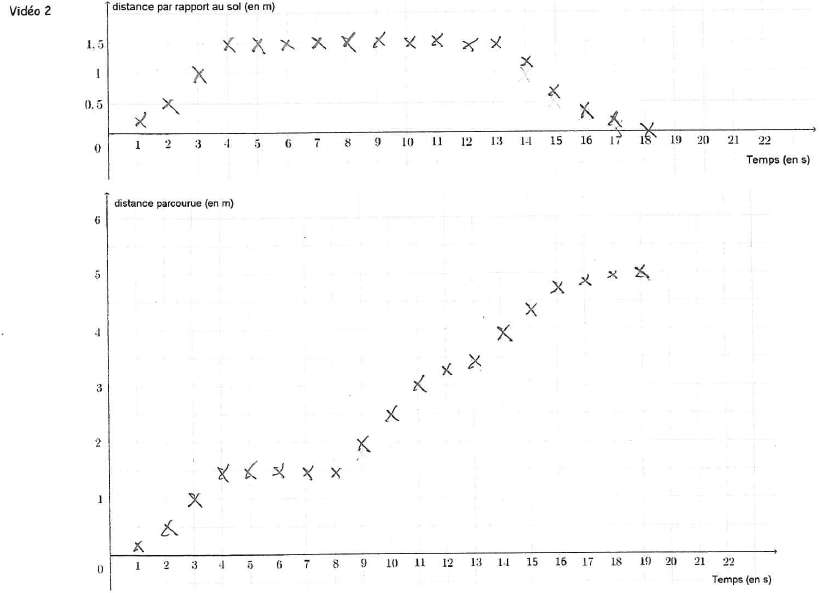
- La hauteur du drone en fonction du temps
- La distance parcourue en fonction du temps
Et inversement, deux situations différentes peuvent être représentées - modélisées par la même courbe.
| Vidéo 1 - stationnaire Vidéo 2 - trajet Vidéo 3 - avance et recule |
Objectifs
Pour la partie 1 :
- Chercher les informations utiles
- Raisonner en analysant le problème
- Calculer une distance avec une échelle
- Calculer une durée en lien avec une vitesse
- Communiquer sa démarche
- Travailler la représentation et la modélisation
- Réinvestir une précédente activité
- Donner du sens à la notion de courbe représentative
Mise en œuvre
Partie 1
Partie 2
- Recherche individuelle pendant 5/10 min
- Travail par deux ou trois pour répondre à la partie 1.
Chaque élève écrit les calculs sur son cahier puis production d’une feuille réponse par groupe pour expliquer la démarche.
Partie 2
- Mise à disposition d’un ordinateur pour accéder aux vidéos et tracer les courbes.
Productions d'élèves pour la partie 1
 |
 |
 |
Productions d'élèves pour la partie construction de courbes
 |
 |
 |
 |
Une correction :
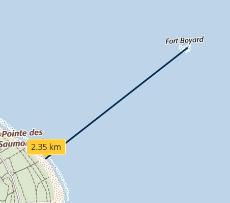 On commence par estimer la distance entre Le Fort Boyard et la plage la plus proche qui se trouve être sur l’île D’Oléron.
On commence par estimer la distance entre Le Fort Boyard et la plage la plus proche qui se trouve être sur l’île D’Oléron.
En regardant la carte proposée par le site Drone-Spot, le survol du fort n’est pas interdit et le vol à partir de la plage au nord de Boyardville est autorisé.
En utilisant l’échelle de la carte :
1,1 cm représente environ 500 m
5,3 cm représente environ 2400 m soit environ 2,4 km.
Distance que l’on peut vérifier avec Geoportail
 On commence par estimer la distance entre Le Fort Boyard et la plage la plus proche qui se trouve être sur l’île D’Oléron.
On commence par estimer la distance entre Le Fort Boyard et la plage la plus proche qui se trouve être sur l’île D’Oléron. En regardant la carte proposée par le site Drone-Spot, le survol du fort n’est pas interdit et le vol à partir de la plage au nord de Boyardville est autorisé.
En utilisant l’échelle de la carte :
1,1 cm représente environ 500 m
5,3 cm représente environ 2400 m soit environ 2,4 km.
Distance que l’on peut vérifier avec Geoportail
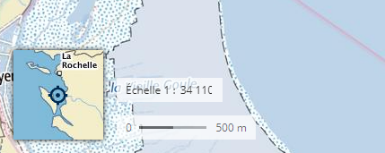 | Remarque : attention à l’utilisation de l’échelle lorsque l’on imprime un document. En effet, si l’on agrandit l’image, la valeur numérique de l’échelle n’est pas changée et n’est donc plus exacte… |
Ce calcul nous permet donc d’éliminer les deux premiers drones car leur distance de transmission est trop faible.
Reste maintenant à vérifier l’autonomie des batteries mais comme l’autonomie des deux derniers drones est similaire, on peut se contenter du drone Xiaomi qui est nettement moins cher.
Pour cela, je préfère ne pas utiliser la vitesse maximale donnée qui doit davantage solliciter la batterie mais celle de 8m/s.
Pour se prendre une petite marge (faire le tour du fort, le vent de face qui se lève…), on peut se fixer une distance à parcourir de 6 km.
8 mètres en 1 s
6000 mètres en 750 s
soit 12 min 30s
Donc l’autonomie semble largement suffisante (même si un test au-dessus d’un champ serait préférable avant de se lancer au-dessus de la mer…)
Partie 2 : Vidéos corrections
| Vidéo 1 - correction Vidéo 2 - correction |
Bilan
Deux courbes identiques peuvent correspondre à des situations différentes.
Pour une même situation, et en fonction d’un même temps, si l’on s’intéresse à deux grandeurs différentes, on peut obtenir des courbes très différentes.
Il est donc très important de mettre les grandeurs sur les axes des abscisses et des ordonnées.
Avant de regarder une courbe, il faut commencer par regarder quelles sont les grandeurs mises en lien.
Pour une même situation, et en fonction d’un même temps, si l’on s’intéresse à deux grandeurs différentes, on peut obtenir des courbes très différentes.
Il est donc très important de mettre les grandeurs sur les axes des abscisses et des ordonnées.
Avant de regarder une courbe, il faut commencer par regarder quelles sont les grandeurs mises en lien.
Arnaud Boulay, enseignant au collège Suzanne Bouteloup, Mayet (72)
information(s) pédagogique(s)
niveau : tous niveaux, 3ème
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

