espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
une mise en place de la dérivation à partir d’un problème de modélisation
mis à jour le 03/06/2020
La dérivation est au cœur des notions à voir en analyse en classe de première que ce soit en première générale ou en première technologique : alors GO !
mots clés : modélisation, dérivation
| Modéliser |
|
Contexte
Classes concernées : groupes de première. La séquence est intervenue assez tôt dans l’année.
La dérivation est au cœur des notions à voir en analyse en classe de première que ce soit en première générale ou en première technologique. En règle générale, les élèves comprennent l’intérêt de la dérivation pour l’étude de fonctions, utilisent les formules de dérivation correctement mais ils éprouvent des difficultés à bien appréhender la définition. Si on peut contourner cette difficulté à court terme, une première approche de la définition est nécessaire et peut passer graphiquement par la position limites des sécantes pour accéder à la tangente.
La modélisation proposée va servir à introduire la notion via le concept physique de vitesse, compréhensible par tous les élèves. C’est ce point de vue cinématique (calcul de fluxion) que Newton (1642 -1727) a développé pour introduire le calcul différentiel et intégral. Leibnitz (1646 -1716) aurait introduit le même concept en utilisant un point de vue plus géométrique (aire de triangles infinitésimaux pour des aires sous des courbes) que cinématique.
Dans un premier temps, la modélisation consiste à interpréter en langage mathématiques une situation réelle, puis d’utiliser le modèle pour développer la dérivation comme un calcul de vitesse instantanée, enfin de s’affranchir du modèle de vitesse pour développer la notion plus globale (limite d’un taux de variations).
La dérivation est au cœur des notions à voir en analyse en classe de première que ce soit en première générale ou en première technologique. En règle générale, les élèves comprennent l’intérêt de la dérivation pour l’étude de fonctions, utilisent les formules de dérivation correctement mais ils éprouvent des difficultés à bien appréhender la définition. Si on peut contourner cette difficulté à court terme, une première approche de la définition est nécessaire et peut passer graphiquement par la position limites des sécantes pour accéder à la tangente.
La modélisation proposée va servir à introduire la notion via le concept physique de vitesse, compréhensible par tous les élèves. C’est ce point de vue cinématique (calcul de fluxion) que Newton (1642 -1727) a développé pour introduire le calcul différentiel et intégral. Leibnitz (1646 -1716) aurait introduit le même concept en utilisant un point de vue plus géométrique (aire de triangles infinitésimaux pour des aires sous des courbes) que cinématique.
Dans un premier temps, la modélisation consiste à interpréter en langage mathématiques une situation réelle, puis d’utiliser le modèle pour développer la dérivation comme un calcul de vitesse instantanée, enfin de s’affranchir du modèle de vitesse pour développer la notion plus globale (limite d’un taux de variations).
Traduire en langage mathématiques une situation réelle
Le problème de départ a été adapté d’un problème trouvé sur le site de l’académie de Paris . Il consiste à donner une courbe d’une fonction où la distance est exprimée en fonction du temps.
Il s’agit ici de traduire en langage mathématiques une situation réelle : y-a-t-il excès de vitesse ou pas ?
Cette activité a été testée plusieurs fois dans différentes classes (ex S et ex ES, 1ère STMG) et cette année (2019-2020) dans deux groupes de première générale. La traduction en langage mathématiques vient très souvent assez vite. Néanmoins la difficulté majeure est le passage de la vitesse moyenne (par exemple sur 1 heure, relativement simple – les élèves répondent alors sur l’excès de vitesse) à la vitesse instantanée c’est-à-dire diminuer encore l’intervalle de temp. La question peut évoluer : à quel moment la vitesse a-t-elle été maximale (un radar prend une vitesse « instantanée ») ? Cette activité, fort riche, est arrêtée relativement tôt néanmoins (gestion d’une plus grande hétérogénéité des élèves), c’est-à-dire une fois le principe acquis qu’il faut diminuer l’intervalle de temps et qu’une tangente est tracée, par exemple au point d’abscisse 3.
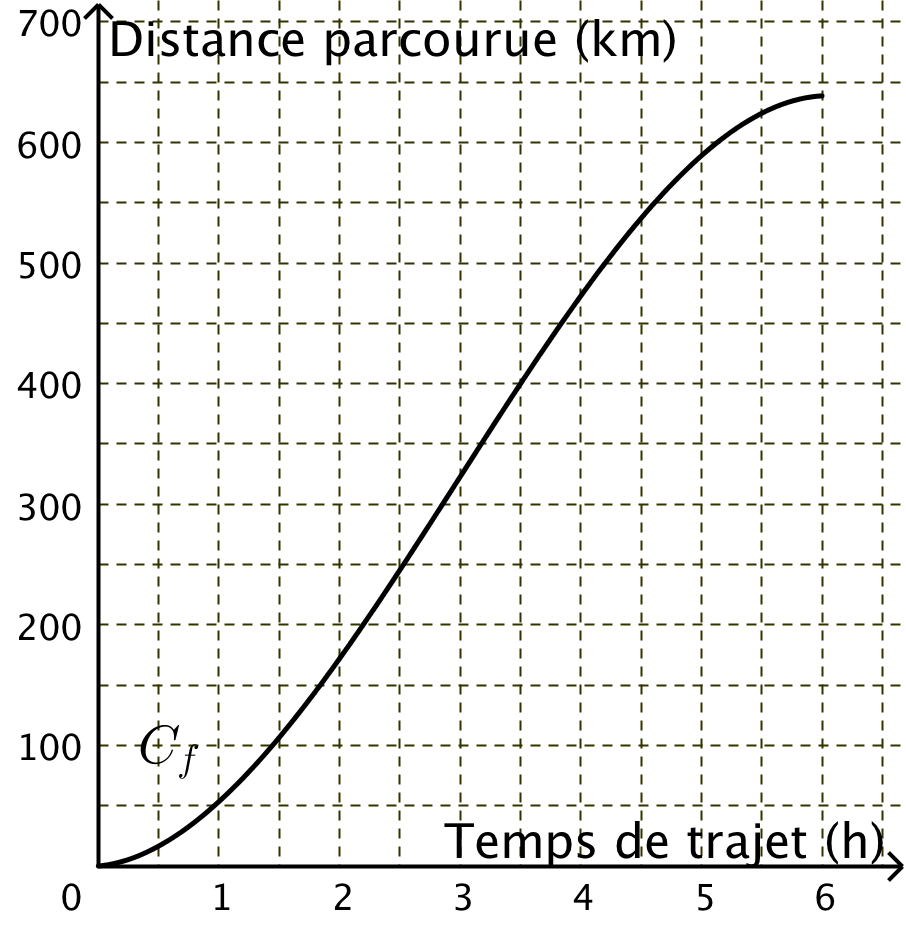 | Un conducteur part pour un long trajet, sur autoroute, d'un peu moins de 640 km et d'une durée totale de 6 h. La courbe ci-dessous représente la fonction qui au temps de trajet « t » (en heure, h) associe la distance parcourue (en km). Les gendarmes l'ont arrêté à la fin de son parcours et l'ont accusé d'avoir fait un excès de vitesse. Le conducteur a argumenté que c'était impossible auprès des gendarmes. |
Il s’agit ici de traduire en langage mathématiques une situation réelle : y-a-t-il excès de vitesse ou pas ?
Cette activité a été testée plusieurs fois dans différentes classes (ex S et ex ES, 1ère STMG) et cette année (2019-2020) dans deux groupes de première générale. La traduction en langage mathématiques vient très souvent assez vite. Néanmoins la difficulté majeure est le passage de la vitesse moyenne (par exemple sur 1 heure, relativement simple – les élèves répondent alors sur l’excès de vitesse) à la vitesse instantanée c’est-à-dire diminuer encore l’intervalle de temp. La question peut évoluer : à quel moment la vitesse a-t-elle été maximale (un radar prend une vitesse « instantanée ») ? Cette activité, fort riche, est arrêtée relativement tôt néanmoins (gestion d’une plus grande hétérogénéité des élèves), c’est-à-dire une fois le principe acquis qu’il faut diminuer l’intervalle de temps et qu’une tangente est tracée, par exemple au point d’abscisse 3.
Utiliser et comprendre une simulation numérique
Afin de garder cette situation dynamique de la vitesse, je propose alors une simulation numérique d’un boulet de canon, trouvée sur le site « Phet » de l’université de Boulder, Colorado, Etats-Unis. Il s’agit de simulations interactives. Le choix se porte sur le mouvement d’un projectile :
Il s’agit là encore de trouver la vitesse instantanée du boulet de canon. Néanmoins ce modèle ne donne pas la hauteur en fonction du temps mais la longueur atteinte au sol par le boulet de canon par rapport à la base en fonction de l’angle et de la vitesse initiale.
Attention, l’objectif n’est pas de comprendre toutes les contraintes physiques proposées mais la situation proposée permet néanmoins de déterminer la vitesse de chute et d’utiliser le modèle précédent. Certaines données sont donc extraites.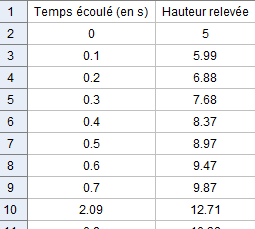 Puis les élèves ont à reconstituer une courbe représentative de la hauteur en fonction du temps (bon rappel du programme de seconde) puis de trouver un moyen de déterminer la vitesse instantanée en un point. Ils utilisent donc une simulation et exploite le modèle proposé à partir de l’excès de vitesse. Cette démarche permet d’acter certaines conventions : la vitesse est ainsi positive lorsque le boulet s’élève et négative lorsqu’il redescend. Cette remarque prendra tout son sens très rapidement lorsque le lien entre le signe de la dérivée et le sens de variations sera « validé ». Remarque : pour quelques élèves, ils peuvent aussi essayer de retrouver la vitesse instantanée à 0 seconde, en utilisant une projection et l’angle – le logiciel proposant une vitesse de 12 m.s-1.
Puis les élèves ont à reconstituer une courbe représentative de la hauteur en fonction du temps (bon rappel du programme de seconde) puis de trouver un moyen de déterminer la vitesse instantanée en un point. Ils utilisent donc une simulation et exploite le modèle proposé à partir de l’excès de vitesse. Cette démarche permet d’acter certaines conventions : la vitesse est ainsi positive lorsque le boulet s’élève et négative lorsqu’il redescend. Cette remarque prendra tout son sens très rapidement lorsque le lien entre le signe de la dérivée et le sens de variations sera « validé ». Remarque : pour quelques élèves, ils peuvent aussi essayer de retrouver la vitesse instantanée à 0 seconde, en utilisant une projection et l’angle – le logiciel proposant une vitesse de 12 m.s-1.
Cette exploitation du modèle se poursuit avec des exercices reprenant systématiquement cette vision de vitesse instantanée.
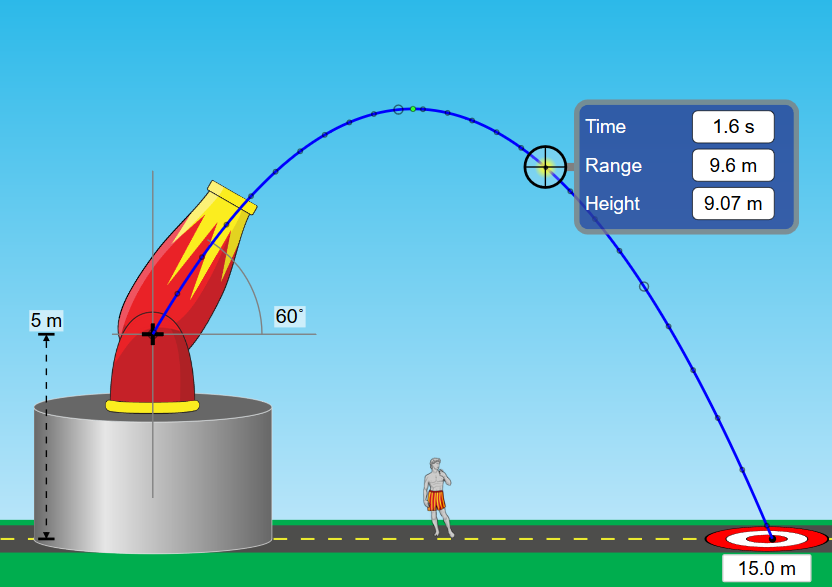 | Pour chaque point indiqué sur le graphique, on peut récupérer le temps (Time) et la hauteur (Height). Objectif : quelle était la vitesse exacte de « chute » du boulet à 1,7 seconde ?
|
Il s’agit là encore de trouver la vitesse instantanée du boulet de canon. Néanmoins ce modèle ne donne pas la hauteur en fonction du temps mais la longueur atteinte au sol par le boulet de canon par rapport à la base en fonction de l’angle et de la vitesse initiale.
Attention, l’objectif n’est pas de comprendre toutes les contraintes physiques proposées mais la situation proposée permet néanmoins de déterminer la vitesse de chute et d’utiliser le modèle précédent. Certaines données sont donc extraites.

Cette exploitation du modèle se poursuit avec des exercices reprenant systématiquement cette vision de vitesse instantanée.
Valider un modèle – vers une définition
La validation du modèle consiste ici à s’affranchir du concept de vitesse physique (distance /temp) pour parvenir à une définition du nombre dérivé en un point d’une fonction continue (variation instantanée des « images » par rapport à la variation instantanée des antécédents ou encore « vitesse instantanée » de l’images en un point). La validation du modèle correspond ici à la mise en place d’une définition d’abord « graphique » dans le cours, puis de la définition avec la limite du taux de variation. Les exercices vont ensuite, petit à petit, s’affranchir de la notion de vitesse instantanée. On peut ainsi proposer des exercices avec l’utilisation du modèle élaboré et le passage ensuite à une représentation. Cela permet ici de développer une autre compétence parfois très proche de la modélisation.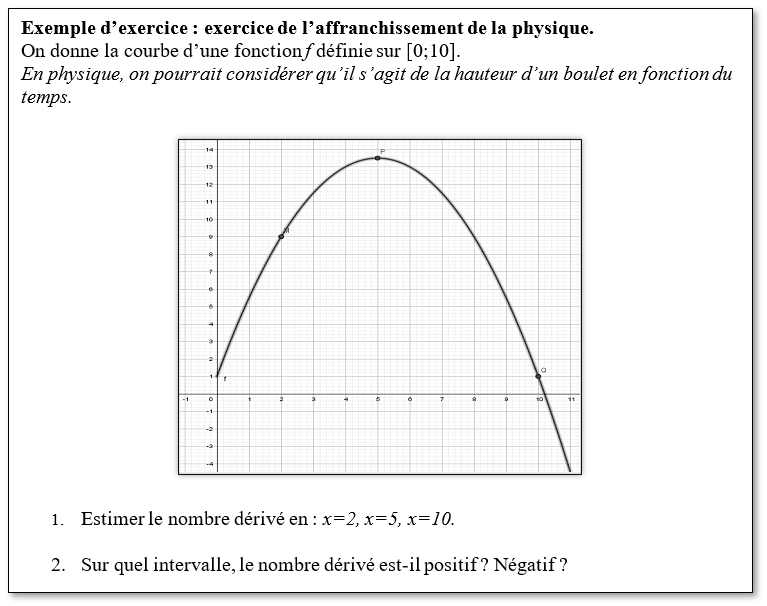

Conclusion
La démarche propose de construire une modèle « physique » de la dérivation avant de s’en détacher. La modélisation, à partir de l’excès de vitesse et du boulet de canon, a permis de comprendre graphiquement le concept de tangente et de le faire vivre. Cette vision met aussi plus rapidement en avant les avantages de la dérivation, à savoir l’étude possible des variations d’une fonction « très sage » (c’est-à-dire se rapportant à une fonction dérivable) à partir du signe de la dérivée sur un intervalle I. Elle permet aussi le décalage de la formalisation correcte, difficile pour certains élèves de première avec la recherche du taux de variations et la limite à déterminer. On peut se plonger un peu plus vite dans l’étude de signes d’une dérivée pour en déduire le sens de variation d’une fonction sur un intervalle.
Fabrice Foucher, enseignant au lycée Jacques Prévert - Savenay (44)
information(s) pédagogique(s)
niveau : tous niveaux, 1ère STG
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
documents complémentaires
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA


