espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
aire d'un étang
mis à jour le 16/11/2021
mots clés : aire, modélisation, TraAM
Voici un extrait d'une activité proposée par Sophie Desruelle lors d'un travail autour de la compétence "modéliser" pour le groupe TraAM de l'académie de Nantes. Cette activité est proposée en sixième, mais des résolutions niveau lycée peuvent mettre en évidence différentes façons de modéliser et éventuellement peuvent permettre de comparer les différents modèles chosis et d'en regarder la pertinence.
Enoncé de l'activité
Voici une cartographie d'un étang.
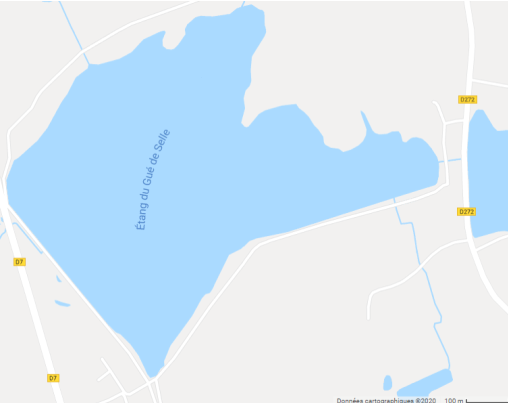
À l’aide d’un papier calque, nous pouvons recouvrir la carte d’un quadrillage de plus en plus fin afin d’avoir un encadrement de l’aire de l’étang.
En utilisant le logiciel Geogebra, voici ce que nous pouvons obtenir :
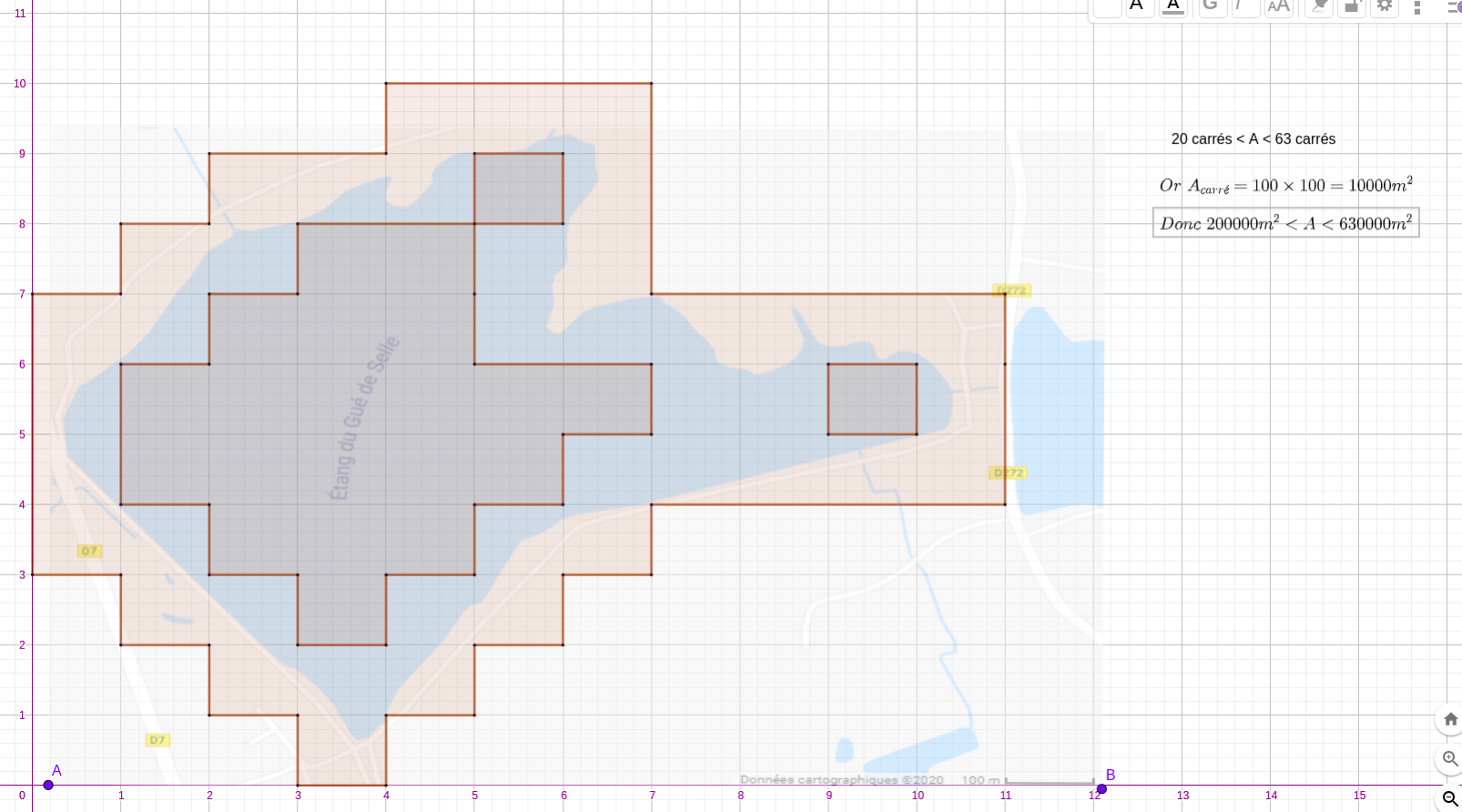
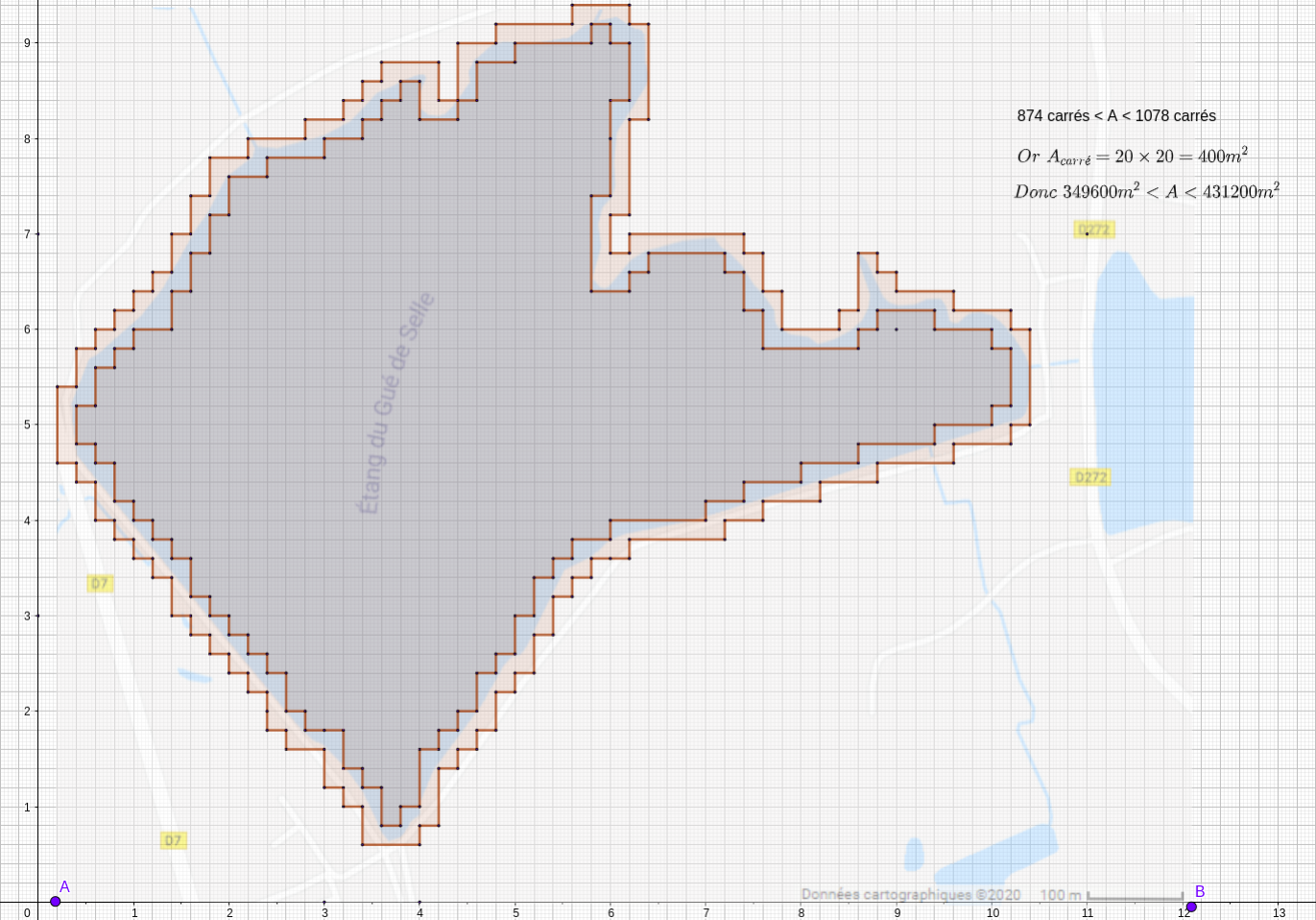
Nous trouvons ainsi : 34,96 ha < Aétang < 43,12 ha.
Ce travail permet de travailler:
- la motricité fine(tracer du quadrillage),
- les échelles,
- l’utilisation d’une unité d’aire pour estimer une aire,
- les conversions d’unités les aires.
Nous pouvons aussi résoudre ce problème avec la méthode de Monté Carlo. Le principe est de "bombarder" un rectangle contenant l’étang avec des points, de façon aléatoire, et de regarder ceux qui tombent à l’eau. Le travail à faire sur Geogebra est assez difficile. Voici les étapes à réaliser :
1. Importer l’image et adapter la taille de l’image ainsi que les unités des axes du repère pour que l’échelle soit facilement utilisable :

2. Tracer un polygone modélisant l’étang :
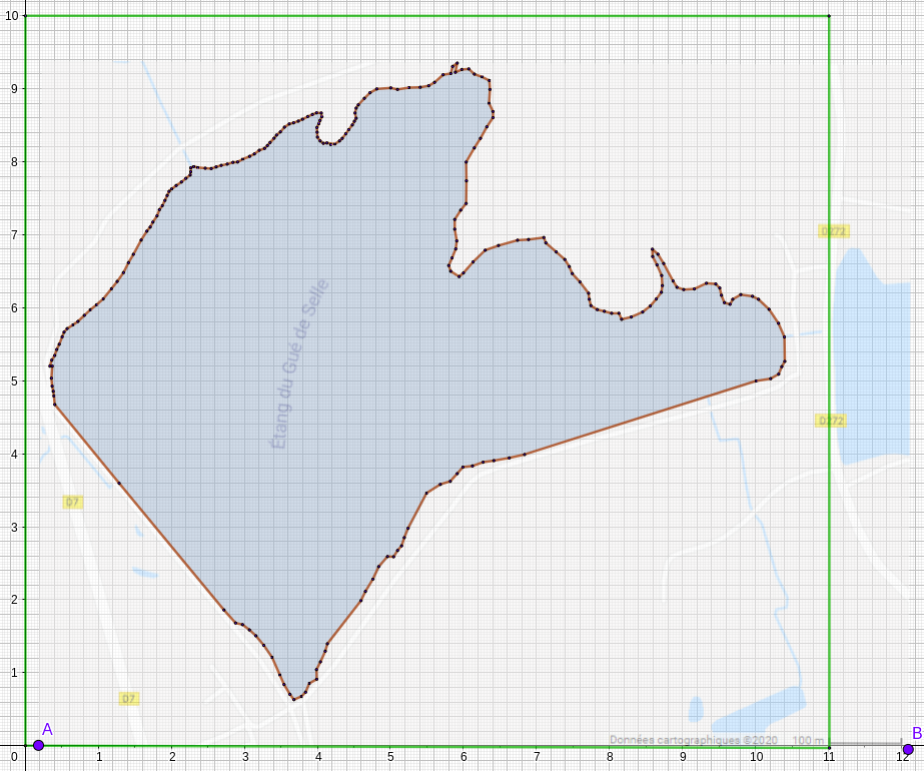
3. Créer un curseur pour faire varier le nombre de points projetés sur la carte :

4. Placer des points de façon aléatoire (en bleu quand ils sont dans l’eau et en vert sinon) et compter le nombre de points qui tombent à l’eau :
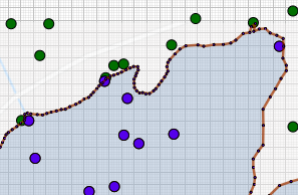
On peut donner aux élèves le fichier préparé par l’enseignent, en affichant juste le nombre de points dans l’eau et le nombre de lancés. Les élèves pourront alors manipuler le curseur, observer les résultats obtenus et débattre sur le choix d’un tel modèle. En quoi permet-t-il d’approximer l’aire de l’étang? Cette activité peut être une première étape avant d’aborder la méthode de Monté Carlo pour approcher l’aire d’un disque (ou approximer pi), ou évaluer l’aire sous une courbe à l’aide d’un programme en Python 1.
Voici un résultat obtenu :
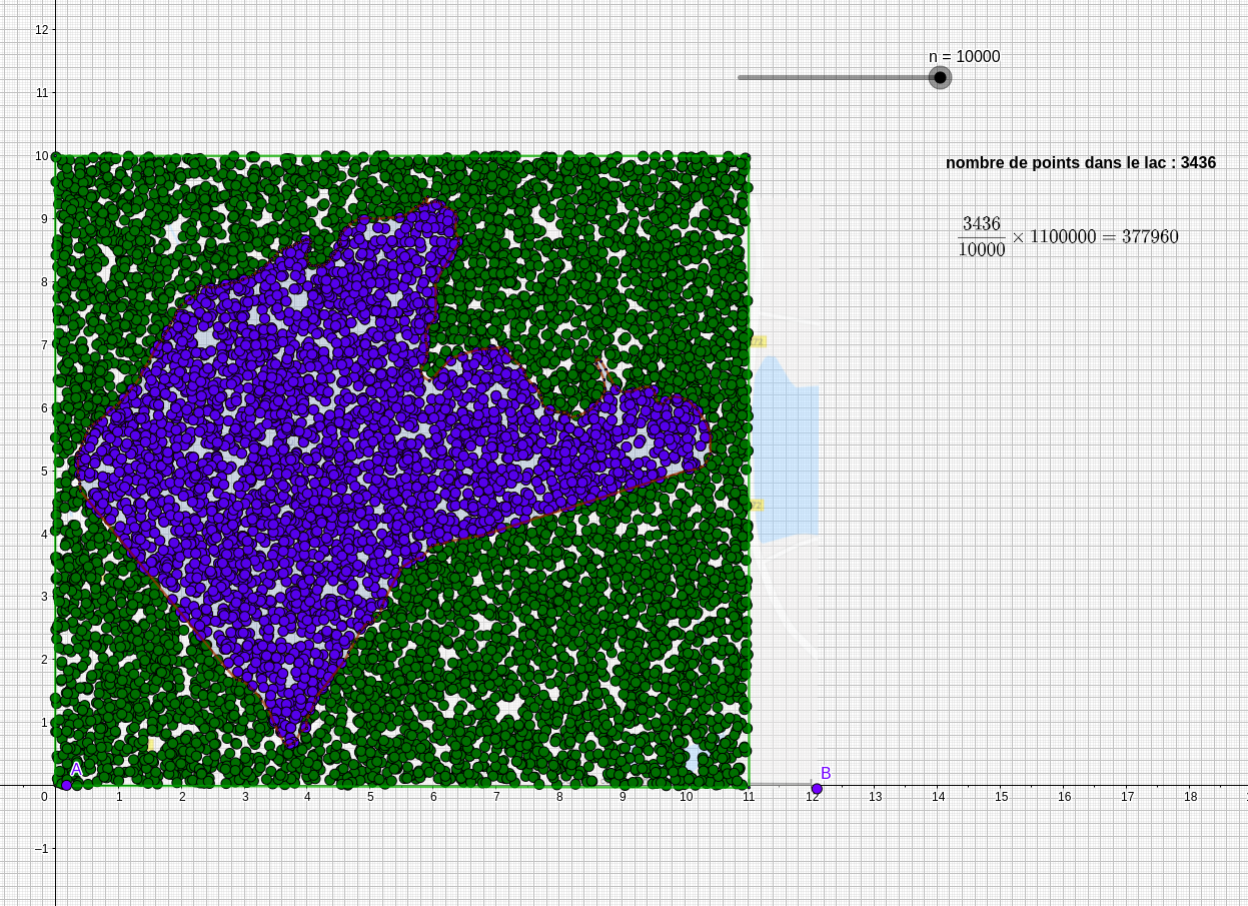
Nous trouvons ainsi : Aétang est environ 37,80 ha
Depuis la rentrée 2019, les élèves de seconde ont tous un enseignement de Sciences Numériques et Technologie. Dans ce programme nous travaillons sur l’image numérique ("Traiter par programme une image pour la transformer en agissant sur les trois composantes de ses pixels"). Avec cette compétence acquise en seconde, nous pouvons donc écrire un programme en Python permettant de compter le nombre de pixels bleus dans l’image et le nombre de pixels au total afin d’estimer l’aire de l’étang.
Première étape :
Il faut que seuls les pixels de l’étang soient en bleus. Avec un logiciel de retouche d’images, (comme Gimp par exemple), on prend le gris de l’image et on peint tout le bleu ne faisant pas partie de l’étang.
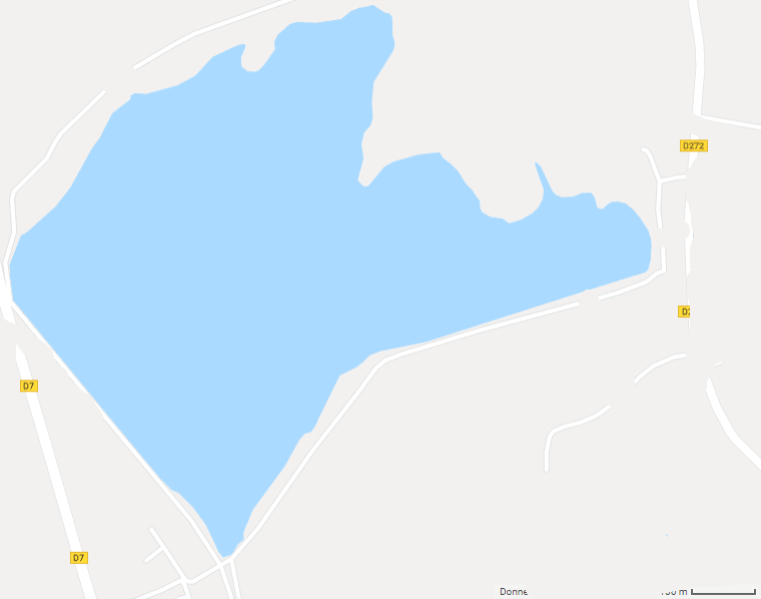
On en profite pour effacer le nom de l’étang et recueillir le code RGB du bleu utilisé (170,218,255).
Programmation :
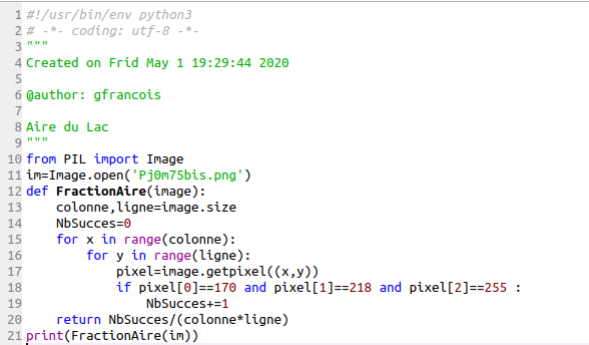
Résultat :

Avec l’échelle, nous pouvons avoir l’aire réelle de l’extrait de carte : 940 x 1 090 = 1 024 600 m2
1024600 x 0, 344 = 352 462, 4
Nous trouvons ainsi : Aétang est environ 35,25 ha
Guillaume François, enseignant au lycée Paul scarron - Sille le Guillaume (72)
information(s) pédagogique(s)
niveau : tous niveaux, Lycée tous niveaux
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
ressource(s) principale(s)

|
modéliser des aires et des volumes | 16/11/2021 |
| Un étang, une voiture et même un rond-point cacahouète... Ca vous tente de les modéliser ? |
||
| volume, aire, modélisation, TraAM | Sophie Desruelle | |
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA