espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
cercle et multiplications
mis à jour le 10/05/2021
mots clés : cercle, modulo, modélisation
Ce travail a été réalisé dans des classes de 4e et de 3e avec une finalité différente.
Les différentes étapes
- Apprendre à utiliser une boucle (travail préparatoire qui peut être proposé avant les séances informatiques pour ne pas perdre de temps)
- Modéliser le cercle (1ère séance)
- Divers tracés (2ème séance de 4e)
- Modéliser les tables de multiplications (2ème séance de 3e)
Apprendre à utiliser une boucle
Tous les élèves n’ayant pas le même niveau (surtout en 4e), il a fallu dans un premier temps apprendre à concevoir une boucle et le principal problème pour eux consiste en l’utilisation d’une variable.
Une idée (mais faut s’entrainer avant pour assurer) :
À partir de là, il est possible d’expliquer que c’est ce que fait l’ordinateur en écrivant les divers résultats, non pas sur une feuille, comme nous, mais dans des variables (compteur1, compteur2, compteur3).
Un peu d’algorithmique débranchée, pour expliquer aux élèves la manière de compter les 10ères valeurs par un programme.

Il est possible de proposer aux élèves de tester un programme qui compte comme travail personnel avec scratch en ligne par exemple.
Une idée (mais faut s’entrainer avant pour assurer) :
- Compter à l’oral de 1 en 1 à partir de 1 ; « 1 ; 2 ; 3 ; 4… »
- Compter à l’oral de 3 en 3 à partir de 4 ; « 4 ; 7 ; 10 ; 13… »
- Reprendre les deux tâches précédentes mais simultanément en invitant les élèves à faire de même « 1/4 ; 2/7 ; 3/10 ; 4/13… » (ne pas lire « un quart, deux septièmes » pour 1/4 ; 2/7, mais « un quatre, deux sept »).
Élèves : « C’est pas simple Monsieur ! » - Proposer de reprendre cet exercice en ajoutant un décompte de -2 en -2 en commençant à 3 « 1/4/3 ; 2/7/-1 ; 3/10/-3 ; 4/13/-6… » (ce qui fait trois listes à lire simultanément).
Élèves : « C’est pas possible, c’est vraiment trop dur ! »
Enseignant : « Pourtant l’ordinateur y arrive très bien avec encore plus de décomptes… » - Possibilité ou non de lancer un programme qui fait exactement ce que nous venons de faire.
Enseignant : Que faudrait-il que nous fassions pour y arriver ? »
Élèves : « Il faudrait que l’on puisse les écrire »
À partir de là, il est possible d’expliquer que c’est ce que fait l’ordinateur en écrivant les divers résultats, non pas sur une feuille, comme nous, mais dans des variables (compteur1, compteur2, compteur3).
Un peu d’algorithmique débranchée, pour expliquer aux élèves la manière de compter les 10ères valeurs par un programme.

Il est possible de proposer aux élèves de tester un programme qui compte comme travail personnel avec scratch en ligne par exemple.
Modéliser le cercle
 Contraintes :
Contraintes :- Demander et/ou conserver le nombre de points sur le cercle dans une variable.
- Utiliser deux listes X et Y pour stocker les coordonnées des points régulièrement espacés sur le cercle.
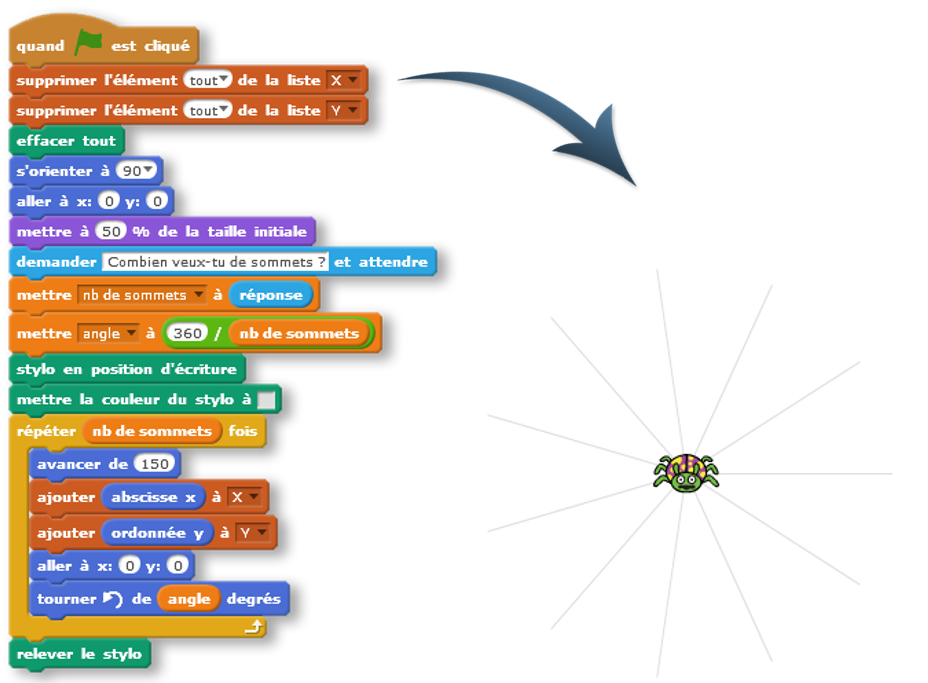
Pour d’autres, ils ont décidé de tracer les rayons du cercle (toujours avec le même problème de calculer à la main l’angle et non pas de créer une formule)
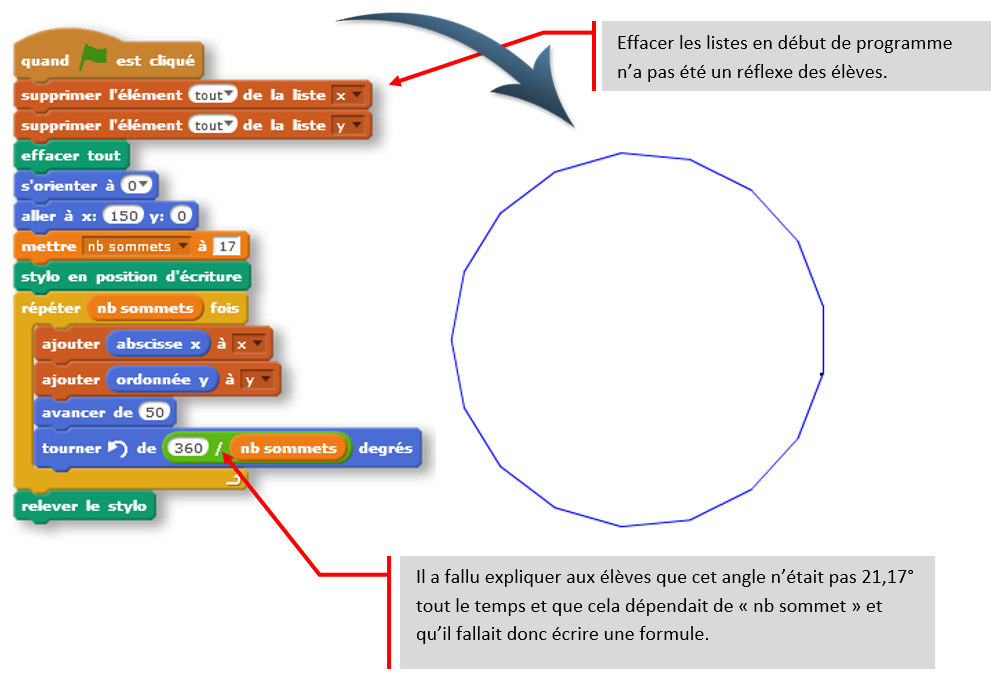
À la fin de l’heure une bonne moitié de la classe avait réussi à modéliser le cercle, l’utilisation de la liste n’ayant pas posé tant de problèmes que cela sauf l'oubli de vider la liste en début de programme.
Divers tracés (4e)
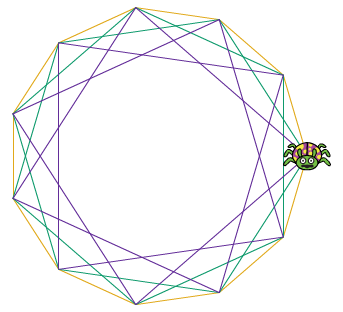 Une fois les points sur le cercle obtenu, les élèves devaient réaliser avec des couleurs différentes le tracé d’un sommet à l’autre, puis en sautant un point à chaque fois, puis en en sautant 2.
Une fois les points sur le cercle obtenu, les élèves devaient réaliser avec des couleurs différentes le tracé d’un sommet à l’autre, puis en sautant un point à chaque fois, puis en en sautant 2.L’utilisation de Bloc (déjà connus pour eux) leur a été recommandée avec pour consigne que seul le bloc avait le droit dessiné.
C’est ici qu’intervient le travail préparatoire que nous avions fait sur le décompte de listes.
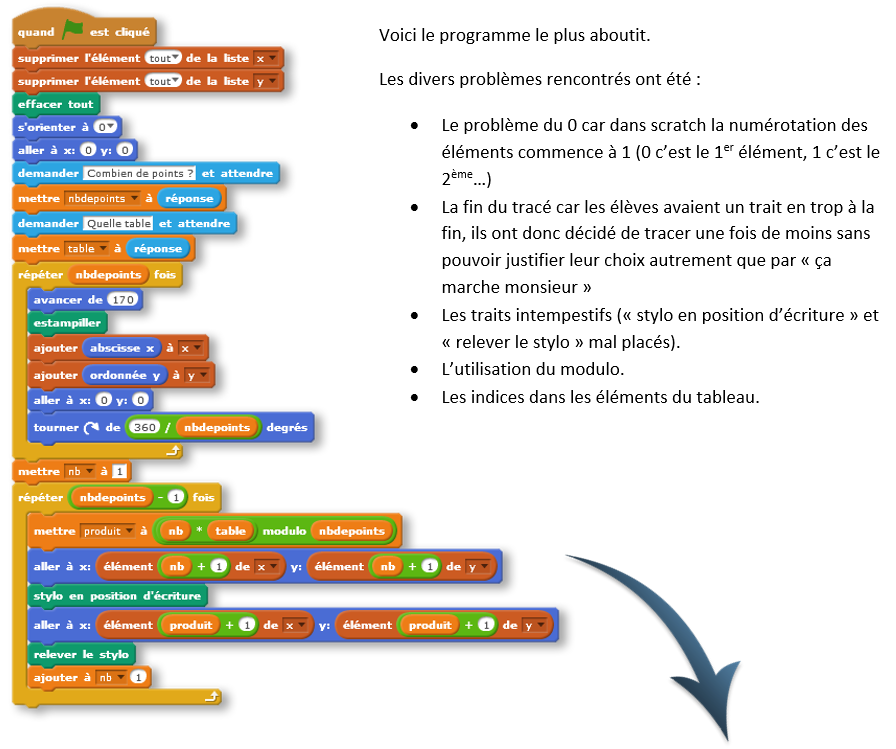
Voici le programme le plus aboutit.
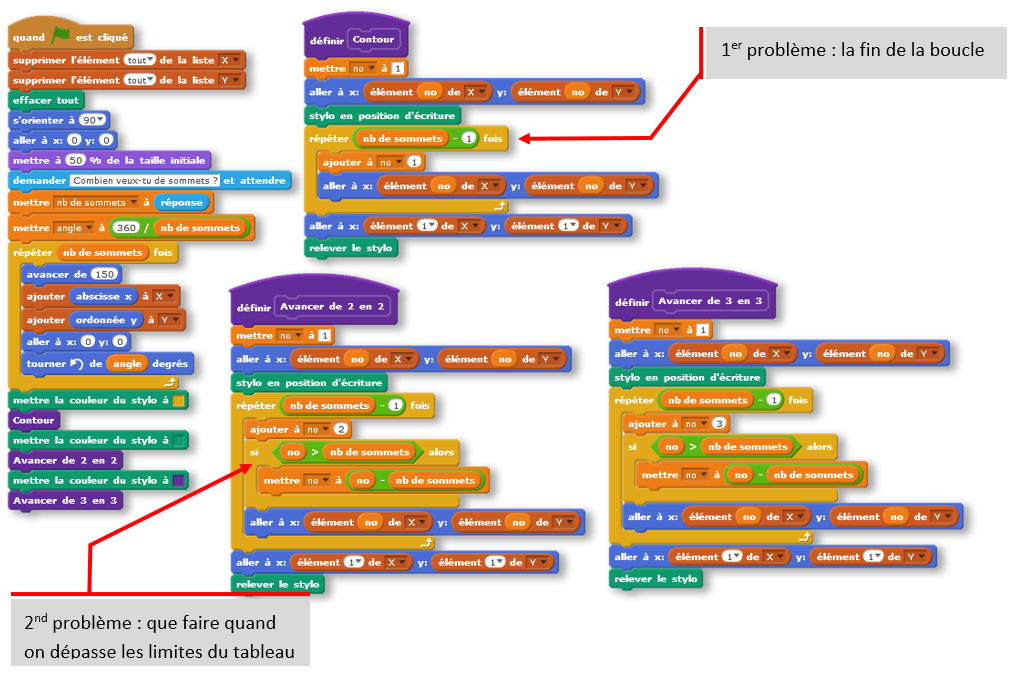
Certains élèves ont passé leur seconde séance à terminer le cercle avec une aide de ma part et n’ont pu que tracer le contour du cercle.
Le binôme qui a réalisé le programme ci-dessus avait très vite compris que les différents blocs étaient quasi identiques (ils ont utilisé le dupliquer de l’ensemble du bloc avec le bouton droit de la souris), je leur ai donc proposé de travailler sur un seul bloc paramétré (de type ci-contre), mais ils n’ont pas eu le temps de finir…
Modéliser les tables de multiplication (3e)
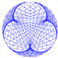
 Après avoir visionné une partie de la vidéo de Mickaël Launey « La face cachée des tables de multiplication » (celle qui ne parle que des nombres entiers, les élèves devaient utiliser leur modélisation du cercle pour réussir à représenter de manière visuelle les tables de multiplication des entiers.
Après avoir visionné une partie de la vidéo de Mickaël Launey « La face cachée des tables de multiplication » (celle qui ne parle que des nombres entiers, les élèves devaient utiliser leur modélisation du cercle pour réussir à représenter de manière visuelle les tables de multiplication des entiers.Afin d’aborder la deuxième séance sereinement, il a fallu revenir sur la division euclidienne en classe et expliquer l’utilisation de l’instruction modulo.

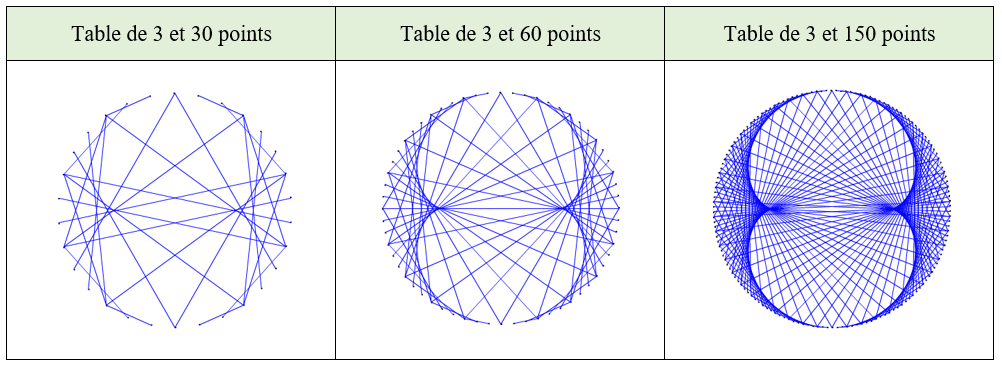
Certains élèves trop en difficulté pour cette deuxième séance ont réalisé ce que j’avais donné aux 4e à savoir le tracé du contour et si possible le tracé en sautant un sommet (puis 2).
Emmanuel Malgras, enseignant au collège Pierre et Marie Curie, Le Pellerin (44)
information(s) pédagogique(s)
niveau : tous niveaux, Cycle 4, 4ème, 3ème
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA