mathématiques
s'identifier
portail personnel ETNA
espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
les ponts en morceaux de bois
mis à jour le 30/04/2021
Si on construisait un pont avec des morceaux de bois entre deux tables ?
mots clés : équation, suite, modélisation
Présentation du problème
La base du problème a été proposée en maths complémentaires et en terminale STMG. Le problème est présenté dans les deux cas à l’oral. Les objectifs étaient toutefois différents. Dans un cas, il s’agissait d’une poursuite du concept de limites de suites en maths complémentaires (le concept aurait été introduit en première si le confinement n’avait pas eu lieu) alors que dans l’autre cas, il s’agit d’introduire spécifiquement la somme des termes d’une suite arithmétique et/ou géométrique. La méthode n’est absolument pas indiquée mais l’objectif commun est bien de modéliser à l’aide de suites numériques le problème posé.
Enoncé du problème : la construction d’un pont entre deux tables.
Les énoncés s’effectuent à l’aide de morceaux de bois pour bien comprendre le principe.
A l’aide de morceaux de bois d’une longueur de 10 cm, construire un pont entre les deux tables avec les règles suivantes :
Précision importante : le principe physique sur le centre de gravité de l’ensemble n’est pas pris en compte. Ainsi, la première pièce peut être collée à la table pour être entièrement dans le vide ou dépasser de 1mm le bord de la table. Le pont ne s’écroule donc pas.
Après une courte recherche individuelle, les élèves sont répartis en groupe de voisinage (par 2 ou 3). Des morceaux de bouts de bois sont distribués dans les différents groupes.
Enoncé du problème : la construction d’un pont entre deux tables.
Les énoncés s’effectuent à l’aide de morceaux de bois pour bien comprendre le principe.
A l’aide de morceaux de bois d’une longueur de 10 cm, construire un pont entre les deux tables avec les règles suivantes :
- La pièce suivante dépassera la pièce précédente en ajoutant 1 mm à chaque fois. Ainsi la deuxième pièce dépasse de 1 mm la première, la troisième pièce dépasse de 2 mm la deuxième, etc…(Uniquement en terminale STMG)
- La pièce suivante dépassera la pièce précédente avec un certain coefficient. Ainsi (par exemple) la deuxième pièce dépasse de 9 cm la première pièce (10% de la longueur totale est enlevée), la troisième pièce dépasse de 8.1 cm la deuxième (soit 10% en moins de 9cm), etc…
Suivant les groupes, on peut faire varier cette proportion toujours en s’appuyant sur une construction physique à l’aide des bouts de bois.
Précision importante : le principe physique sur le centre de gravité de l’ensemble n’est pas pris en compte. Ainsi, la première pièce peut être collée à la table pour être entièrement dans le vide ou dépasser de 1mm le bord de la table. Le pont ne s’écroule donc pas.
Après une courte recherche individuelle, les élèves sont répartis en groupe de voisinage (par 2 ou 3). Des morceaux de bouts de bois sont distribués dans les différents groupes.
Recherche des élèves et modélisation
Très vite, les élèves s’emparent des morceaux de bois pour commencer leur pont.
En maths complémentaires, la modélisation par les suites arrive assez naturellement. Le problème revient donc à déterminer si la somme des bouts de bois comble l’espace entre les deux tables (ou le ½ espace car certains souhaitent partir des deux côtés).
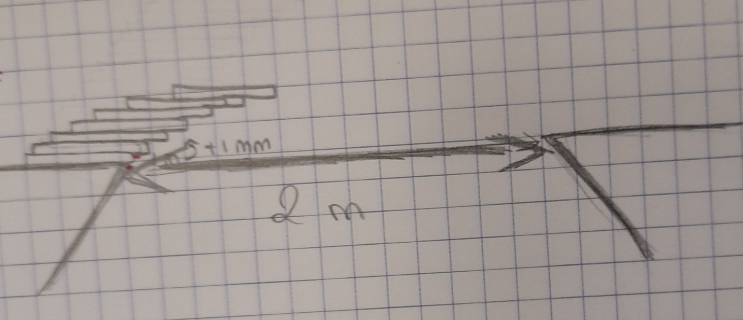
On peut remarquer que la représentation ne correspond pas à la suite géométrique. Sur la représentation, ce qui dépasse correspond toujours au 2/3 de l’espace précédent.
En terminale STMG, pour la très grande majorité des groupes, un temps de manipulation est nécessaire afin de bien comprendre ce qui est demandé.
Puis, de nombreux dessins apparaissent pour bien comprendre ce qui est demandé.
Enfin, après mes relances pour associer la représentation à un modèle mathématique, le modèle de « suites numériques » apparait.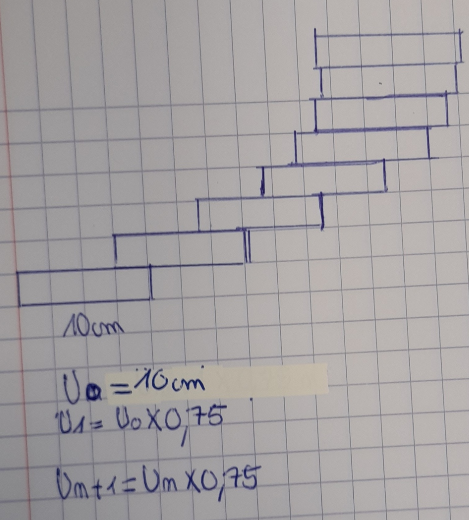
En maths complémentaires, la modélisation par les suites arrive assez naturellement. Le problème revient donc à déterminer si la somme des bouts de bois comble l’espace entre les deux tables (ou le ½ espace car certains souhaitent partir des deux côtés).
On peut remarquer que la représentation ne correspond pas à la suite géométrique. Sur la représentation, ce qui dépasse correspond toujours au 2/3 de l’espace précédent.
En terminale STMG, pour la très grande majorité des groupes, un temps de manipulation est nécessaire afin de bien comprendre ce qui est demandé.
Puis, de nombreux dessins apparaissent pour bien comprendre ce qui est demandé.
Enfin, après mes relances pour associer la représentation à un modèle mathématique, le modèle de « suites numériques » apparait.
Bilan : Une modélisation pour quoi faire ?
- Traduire en langage mathématique une situation réelle (à l’aide d’équations, de suites,
de fonctions, de configurations géométriques, de graphes, de lois de probabilité, d’outils statistiques...). - Utiliser, comprendre, élaborer une simulation numérique ou géométrique prenant appui sur la modélisation et utilisant un logiciel. Le tableur (STMG) ou un algorithme (STMG / Maths complémentaires) ont été utiles pour permettre de donner une réponse à ce problème avant d’utiliser les limites ou la somme des termes.
- Valider un modèle.
En maths complémentaires, le problème a été réexploité avec des données différentes.
- …Ou invalider un modèle.
Les problèmes ne sont que purement théoriques…un pont ne peut pas tenir physiquement…sauf à utiliser la suite harmonique (prolongement possible – fait en maths complémentaires).
lien : https://www.lebesgue.fr/video/5min/tapie-viola
Fabrice Foucher, enseignant au lycée Jacques Prévert, Savenay (44)
information(s) pédagogique(s)
niveau : tous niveaux
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
documents complémentaires
| Fichier(s) associé(s) |
 la présente activité. |
mathématiques - Rectorat de l'Académie de Nantes