espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2021-2022
les fonctions s'éclatent façon puzzle
mis à jour le 21/06/2022
Faire présenter, par un élève, un travail sur une fonction de référence devant un jury composé des membres des autres groupes.
mots clés : oral, fonction, actions académiques, labo maths
En classe entière, les élèves sont répartis en groupe de 4 ou 5. Chaque groupe reçoit des consignes précises de travail sur une des fonctions de références : la fonction carrée, la fonction cube, la fonction inverse, la fonction racine carrée et les fonctions affines.
Des points de compréhension précis sont attendus et des questions sont posées afin de les guider. Chaque groupe doit produire une affiche qui servira de support à la fois pour la présentation orale et à la fois pour le cours écrit.
La séquence s’est répartie sur 3 heures : 2 heures pour le travail en groupe (et même pour certains à finaliser chez eux) et une heure de présentation orale.
Pour la restitution orale, les groupes sont recomposés (chaque nouveau groupe comporte un membre du groupe initial) et répartis dans divers endroits de la salle polyvalente où tour à tour, ils seront rapporteurs ou membres du jury.
Un exemple de fiche donné au groupe
Les fiches sont toutes conçues sur le même modèle. Voici celle sur la fonction carrée.
La fonction carrée


Quelques éléments d’analyse de la séquence
Voici quelques points observés qui méritent réflexion :
Sur la partie orale, il est extrêmement compliqué d’avoir une vision globale et pertinente des prestations des élèves répartis dans la salle.
Par rapport à l’expérimentation précédente, chaque jury disposait de deux questions à poser au présentateur. Ces questions étaient identiques (aux nombres près) au travail de préparation demandé.
Chaque jury devait poser les questions adaptées à la présentation.

Bien que n’ayant pu matériellement suivre tous les oraux, j’ai constaté sur un oral particulier que le présentateur n’a pas pu répondre à ces questions, ni même produire une explication identique à celle de la présentation
Ce travail a été immédiatement suivi de questions, en classe entière, liés à la reconnaissance de ces fonctions ou à la résolution graphique d’équations. Force est de constater que les élèves ont retenu peu d’éléments du travail effectué, à l’exception peut-être d’une meilleure maîtrise de la notion d’images et d’antécédents.
BilanCompétences développées
Compétences mathématiques en lien avec cette activité :
Communiquer Raisonner Calculer Représenter Exemples de travaux d’élèves
Des points de compréhension précis sont attendus et des questions sont posées afin de les guider. Chaque groupe doit produire une affiche qui servira de support à la fois pour la présentation orale et à la fois pour le cours écrit.
La séquence s’est répartie sur 3 heures : 2 heures pour le travail en groupe (et même pour certains à finaliser chez eux) et une heure de présentation orale.
Pour la restitution orale, les groupes sont recomposés (chaque nouveau groupe comporte un membre du groupe initial) et répartis dans divers endroits de la salle polyvalente où tour à tour, ils seront rapporteurs ou membres du jury.
Les fiches sont toutes conçues sur le même modèle. Voici celle sur la fonction carrée.
La fonction carrée


Voici quelques points observés qui méritent réflexion :
- La fiche sur les fonctions affines s’est révélée trop complexe à gérer pour les élèves et les autres fiches représentaient un travail déjà suffisant. De même, la partie « pour aller plus loin » n’est pas nécessaire.
- Les groupes ont tous eu des difficultés à comprendre la notion d’ensemble de définition, ce qui a nécessité l’intervention dans tous les groupes de l’enseignant. Cela a occasionné un retard certain sur le temps dévolu à l’activité.
- Chaque groupe devait réaliser un support pour que chaque membre puisse s’appuyer dessus pour la présentation orale qui devait suivre comme indiqué dans les consignes.
Sur la partie orale, il est extrêmement compliqué d’avoir une vision globale et pertinente des prestations des élèves répartis dans la salle.
Par rapport à l’expérimentation précédente, chaque jury disposait de deux questions à poser au présentateur. Ces questions étaient identiques (aux nombres près) au travail de préparation demandé.
Chaque jury devait poser les questions adaptées à la présentation.

Bien que n’ayant pu matériellement suivre tous les oraux, j’ai constaté sur un oral particulier que le présentateur n’a pas pu répondre à ces questions, ni même produire une explication identique à celle de la présentation
Ce travail a été immédiatement suivi de questions, en classe entière, liés à la reconnaissance de ces fonctions ou à la résolution graphique d’équations. Force est de constater que les élèves ont retenu peu d’éléments du travail effectué, à l’exception peut-être d’une meilleure maîtrise de la notion d’images et d’antécédents.
Bilan
Les élèves ont apprécié ce type de travail et notamment l’autonomie qu’ils ont eue.
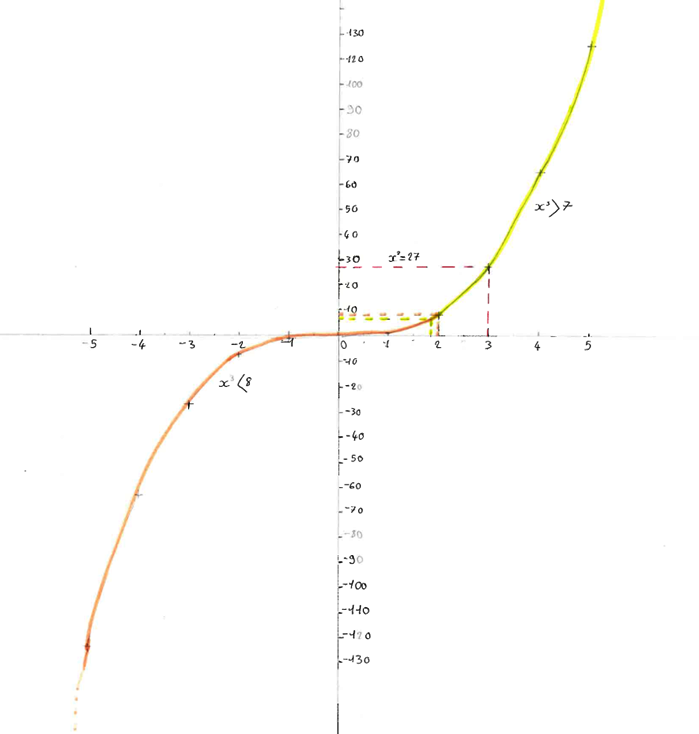
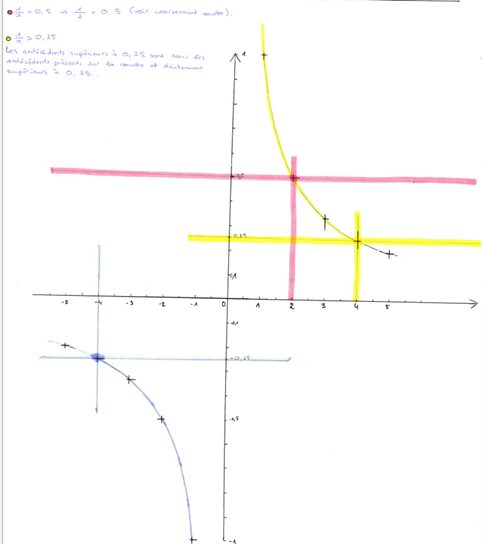
Les fiches conçues par les élèves ont servi de support de cours et ont été complétées ou corrigées. La résolution graphique d’équations et d’inéquations a été reprise en classe, avec une oralisation importante de la méthode de recherche des solutions.
Les fiches conçues par les élèves ont servi de support de cours et ont été complétées ou corrigées. La résolution graphique d’équations et d’inéquations a été reprise en classe, avec une oralisation importante de la méthode de recherche des solutions.
Compétences mathématiques en lien avec cette activité :
Les présentations orales furent un cadre privilégié pour permettre aux élèves de s’exprimer avec clarté et précision à l’oral.
Les résolutions d’équations demandaient un raisonnement en lien avec le vocabulaire des fonctions.
L’activité demandée mettait en jeu des notions liées aux calculs numériques.
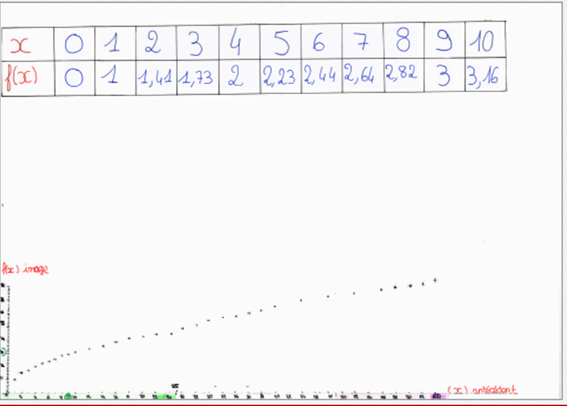
L’activité proposée demandait de construire les représentations graphiques des fonctions de référence.



Grégory Maupu, enseignant au lycée François Truffaut à Challans(85)
information(s) pédagogique(s)
niveau : tous niveaux, 2nde
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

