espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2021-2022
oral - divers problèmes
mis à jour le 20/06/2022
Faire présenter, par un élève, un travail sur une fonction de référence devant un jury composé des membres des autres groupes.
mots clés : oral, actions académiques, labo maths
Durant l'heure dédoublée, les élèves sont répartis en groupe de 4 ou 5, avec pour but de travailler sur l'exercice de modélisation fournis dans le but d'une présentation future aux autres groupes.
Chaque groupe dispose d'un exercice d'optimisation géométrique différent, l'objectif sous-jacent est de parvenir à une algébrisation du problème.
Pour la restitution orale, les groupes sont recomposés (chaque nouveau groupe comporte un membre du groupe initial) et répartis dans divers salles où tour à tour, ils seront rapporteur ou jury.
1 Les exercices donnés au groupe
Les exercices portent tous sur une situation géométrique où un des points de la figure est mobile. Il s'agit donc de figure dynamique conduisant à une recherche de valeur.
Dans l'absolu, il s'agit d'être amené à trouver la solution d'une équation ou de trouver l'extremum d'une fonction.
2 Quelques éléments d'analyse de la séquence
Initialement prévu pour durer une heure, la séquence s'est étalée sur deux heures. Voici quelques points observés qui méritent réflexion :
Bilan
Les élèves ont apprécié ce type de travail et notamment l'autonomie qu'ils ont eu.
Ensuite, la mise en commun des problèmes a eu lieu. J'ai mis en évidence une méthodologie commune pour les résoudre. On a dégagé les grandes étapes de résolution et travaillé sur l'algébrisation.
3 Compétences développées
Compétences mathématiques en lien avec cette activité :
Communiquer :
Les présentations orales furent un cadre privilégié pour permettre aux élèves de s'exprimer avec clarté et précision à l'oral et à l'écrit mais aussi de développer une argumentation mathématique la plus rigoureuse possible.
Chercher et raisonner :
La résolution demandait une recherche et/ou un raisonnement en lien avec des notions vues au collège.
Calculer :
L'activité demandée mettait en jeu des notions liées aux calculs numériques, à la relation de Pythagore ou aux équations.
Modéliser :
L'activité proposée permettait de traduire en langage mathématique une situation issue des mathématiques.
4 Exemples de travaux d'élèves

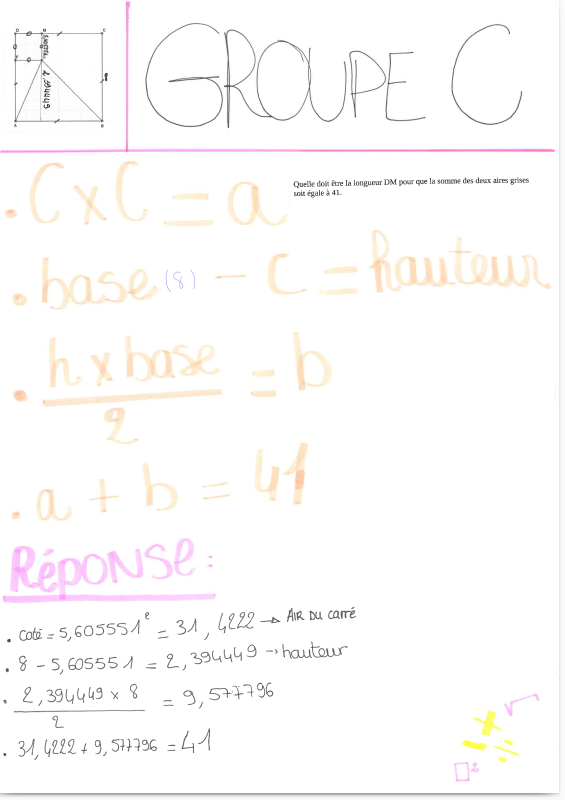

Chaque groupe dispose d'un exercice d'optimisation géométrique différent, l'objectif sous-jacent est de parvenir à une algébrisation du problème.
Pour la restitution orale, les groupes sont recomposés (chaque nouveau groupe comporte un membre du groupe initial) et répartis dans divers salles où tour à tour, ils seront rapporteur ou jury.
1. Les exercices donnés
2. Quelques éléments d'analyse de la séquence
3. Compétences développées
4. Exemples de travaux d'élèves
2. Quelques éléments d'analyse de la séquence
3. Compétences développées
4. Exemples de travaux d'élèves
Les exercices portent tous sur une situation géométrique où un des points de la figure est mobile. Il s'agit donc de figure dynamique conduisant à une recherche de valeur.
Dans l'absolu, il s'agit d'être amené à trouver la solution d'une équation ou de trouver l'extremum d'une fonction.
| Problème (Groupe A) [AB] est un segment de 10 cm. On place un point M, au hasard sur [AB]. Le point M est mobile. On obtient la figure suivante où :
Quelle doit être la longueur AM pour que le carré et le triangle ait le même périmètre ? | 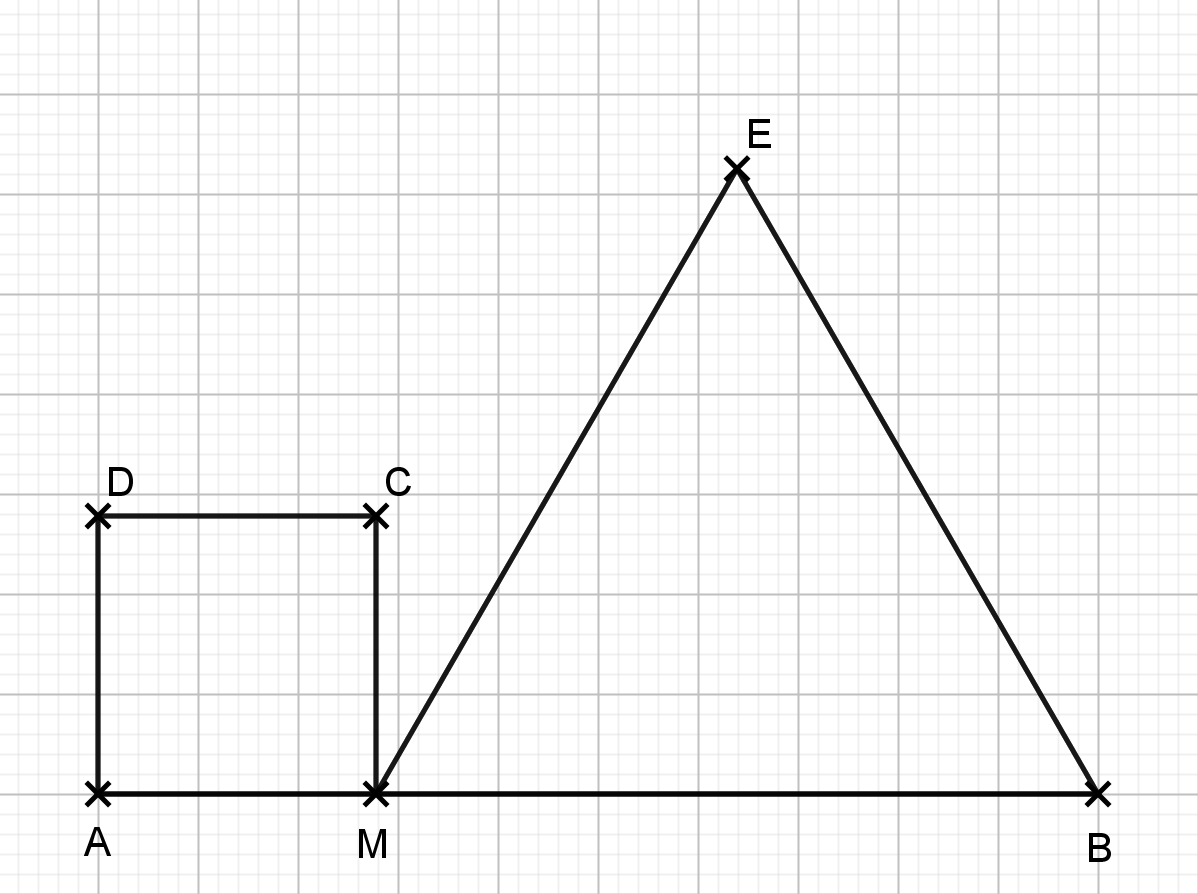 |
| Problème (Groupe B) [AB] est un segment de 10 cm. On place un point M, au hasard sur [AB]. Le point M est mobile. On obtient la figure suivante où :
Quelle doit être la longueur AM pour que le carré et le triangle ait la même hauteur ? | 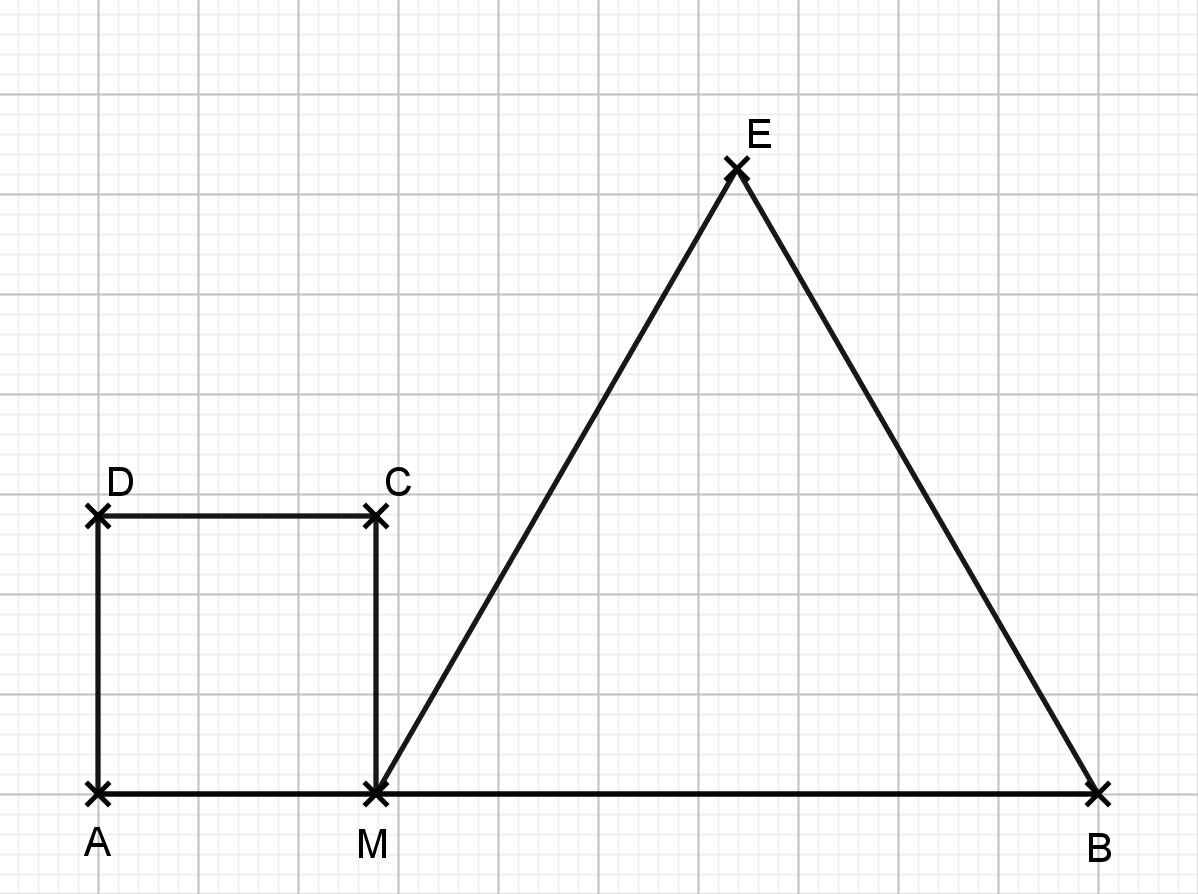 |
| Problème (Groupe C) ABCD est un carré de côté 8. On place un point M, au hasard sur [CD]. Le point M est mobile. DMGF est un carré et ABG est un triangle. Quelle doit être la longueur DM pour que la somme des deux aires grises soit égale à 41. | 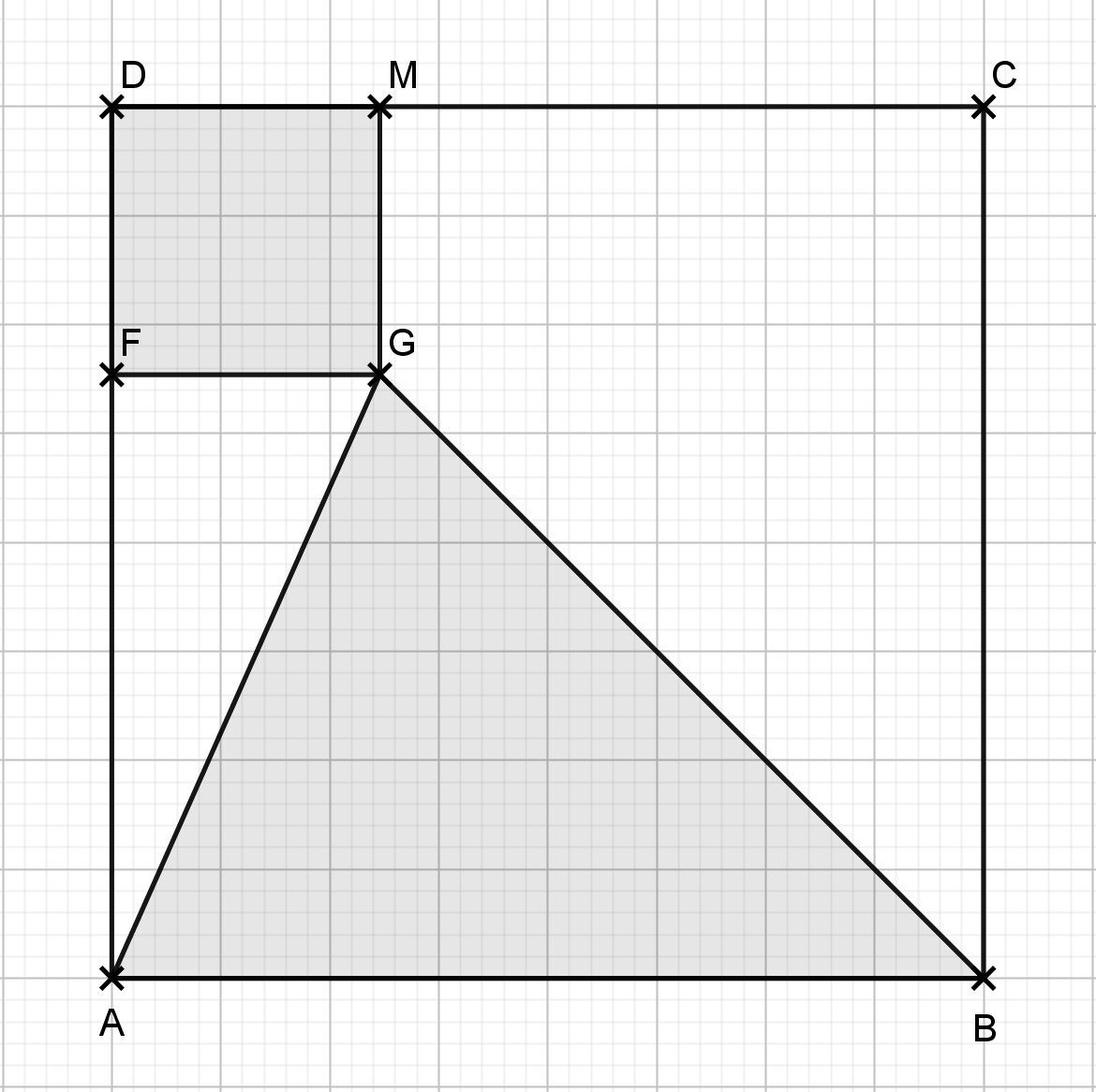 |
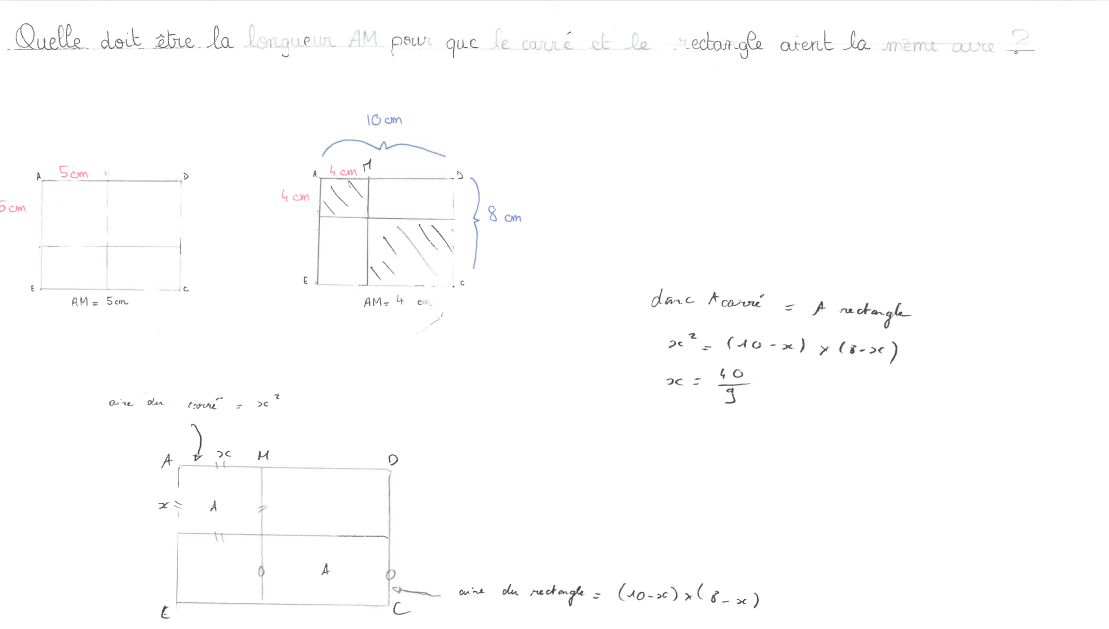
| Problème (Groupe D) ADCE est un rectangle tel que AD = 10 et AE = 8 On place un point M, au hasard sur [AD]. Le point M est mobile. AMPQ est un carré et PTCR est un rectangle. Quelle doit être la longueur AM pour que le carré et le rectangle ait la même aire ? | 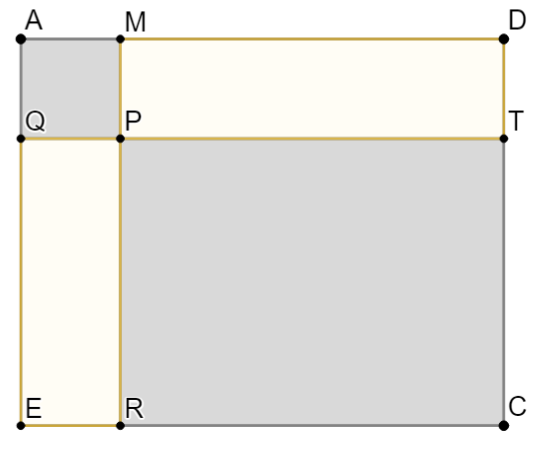 |
Initialement prévu pour durer une heure, la séquence s'est étalée sur deux heures. Voici quelques points observés qui méritent réflexion :
- Les élèves se sont engagés de manière importante dans la recherche de l'inconnue et l'aspect oral à l'intérieur des groupes s'est révélé très important.
- Seul un groupe (en fait deux élèves dans le même groupe) a algébrisé le problème.
- Chaque groupe devait réaliser un support pour que chaque membre puisse s'appuyer dessus pour la présentation orale qui devait suivre.
- Sur la partie orale de restitution, il est extrêmement compliqué d'avoir une vision globale et pertinente des prestations des élèves répartis dans des salles différentes mais j'ai pu noter deux points :
- L'élève qui avait algébrisé le problème avait aussi une vision très claire des différentes étapes de résolution et était capable de les dégager lors de sa présentation ;
- Beaucoup de présentation se focalise sur la suite des calculs effectués et sur le résultat (même avec 10 décimales). Aucune hauteur n'est prise et on peut s'interroger sur la compréhension du problème.
- Chaque jury disposait d'une grille afin de pouvoir observer certains points de la prestation orale (tant sur la posture que sur l'aspect mathématique). On peut remarquer que :
- Les élèves sont très bienveillants entre eux et ont même des difficultés à émettre un avis « négatif » (une élève est venue presque s'excuser que leur jury ait mis insuffisant à une présentation).
- Le travail sur un problème similaire et la pratique des mathématiques depuis des années ne suffit pas à les rendre « expert ». Il semble nécessaire de préparer ce type de travail en amont sur deux aspects dans un travail du quotidien en classe : la mise en évidence des attendus sur l'oral et la mise en évidence de l'attendu mathématique.
Bilan
Les élèves ont apprécié ce type de travail et notamment l'autonomie qu'ils ont eu.
Ensuite, la mise en commun des problèmes a eu lieu. J'ai mis en évidence une méthodologie commune pour les résoudre. On a dégagé les grandes étapes de résolution et travaillé sur l'algébrisation.
Compétences mathématiques en lien avec cette activité :
Communiquer :
Les présentations orales furent un cadre privilégié pour permettre aux élèves de s'exprimer avec clarté et précision à l'oral et à l'écrit mais aussi de développer une argumentation mathématique la plus rigoureuse possible.
Chercher et raisonner :
La résolution demandait une recherche et/ou un raisonnement en lien avec des notions vues au collège.
Calculer :
L'activité demandée mettait en jeu des notions liées aux calculs numériques, à la relation de Pythagore ou aux équations.
Modéliser :
L'activité proposée permettait de traduire en langage mathématique une situation issue des mathématiques.

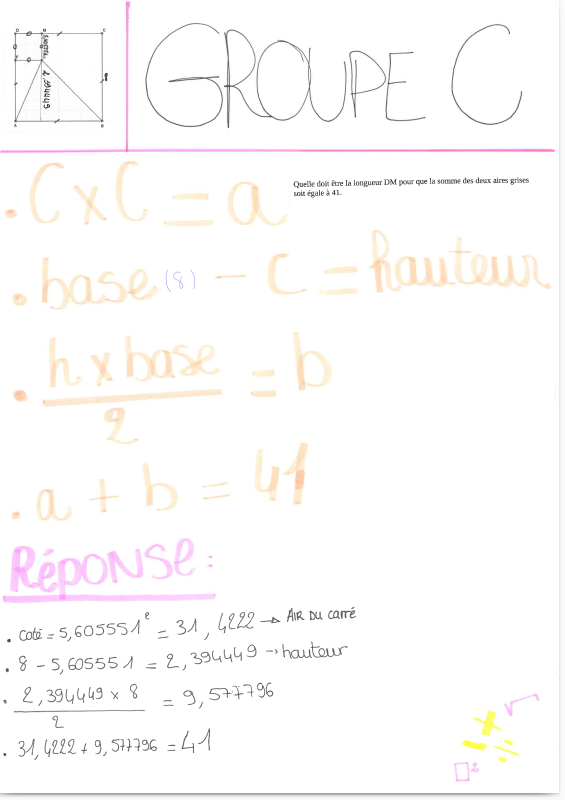


Grégory Maupu, enseignant au lycée François Truffaut à Challans(85)
information(s) pédagogique(s)
niveau : tous niveaux, 2nde
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA

