espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2021-2022
quand l'oral peut servir l'écrit
mis à jour le 02/06/2022
Une expérimentation qui a pour point de départ des remarques ou d’écrits de certains élèves de 4ème / 3ème.
mots clés : oral, calcul littéral, actions académiques
Le point de départ de l’expérimentation vient de remarques ou d’écrits de certains élèves de 4ème / 3ème.
Voici quelques remarques entendues dans nos cours :
- « Je ne sais plus 3x c’est 3+x ou 3×x ? »,
- « Pour passer de x à 3x il suffit de faire +3 ! »
- …
A l’écrit il n’est pas rare de voir des élèves qui notent : 3x = 35 si x=5.
Le passage de 3x à 3×x ou inversement de 3×x à 3x semble loin d’être acquis pour certains de nos élèves en fin de cycle 4.
L’idée est d’essayer d’asseoir cette notion dès la 5ème . Après avoir introduit la lettre et notamment travaillé sur remplacer une lettre par un nombre dans une expression littérale, nous avons voulu essayer de passer par l’oral avant de revenir à l’écrit.
Dans ce premier temps nous avons gardé les signes opératoires, et nous avons juste travaillé le remplacement d’une lettre par un nombre :
- Déterminer la valeur de A=3+5×r quand r=4.
- L’égalité 2×a+3=6×a est-elle vraie pour a=5 ?
- …
Cette étape a duré 2 mois et le travail effectué, lors de la 1ère étape, sur le remplacement d’une lettre par un nombre avec les signes opératoires a été entretenu en activité flash.
Au début de chaque heure de cours une question énoncée uniquement à l’oral est donnée. La consigne donnée aux élèves est : « vous n’avez rien le droit d’écrire sur votre cahier à part la réponse ».
- « J’achète des albums. Combien vaut 3a si a=10 »
- « Je fais des tours sur une piste d’athlétisme. Combien vaut 5t si t=100 »
- « Je mange des bonbons. Combien vaut 25-b si b = 4 »
- …
Lors de ces questions seul(s) 1 ou 2 élève(s) par classe donne(nt) une réponse erronée. La correction écrite par l’enseignant avait toujours la même forme :
- Réécrire la consigne :
- Ecrire le calcul fait et la réponse :
- Préciser à l’oral « en fait on a fait 3 fois a »
- « Combien vaut 6+r si r=7 »
- « Combien vaut 5t si t=8 »
- « Combien vaut 4x si x=1,5 »
- « Combien vaut 5k+6 si k=2 »
- …
Là encore très peu, voire pas du tout, d’erreur commise par les élèves, au moins sur le fait de multiplier (nous n’avons pas tenu compte des erreurs de calcul). La correction se déroule exactement comme précédemment.
- « Combien vaut x pour que 4x=20 »
- « Combien vaut d pour que d+3=7 »
- « Combien vaut h pour que 3h=36 »
- …
Un mois se passe, pendant lequel on arrête les questions orales mais on continue à entretenir le remplacement d’une lettre par un chiffre dans une expression contenant les signes opératoires.
Nous décidons alors de voir, si les élèves peuvent se passer de signe opératoire à l’écrit.
Voici les exercices proposés avec des réponses proposées par les élèves :
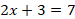 | 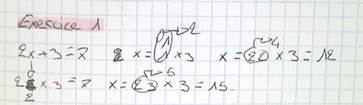 L’écriture n’est pas correcte (il manque le signe « × ») mais l’élève fait bien une multiplication : pour x=2 2x devient 22 il fait cependant 2×2. 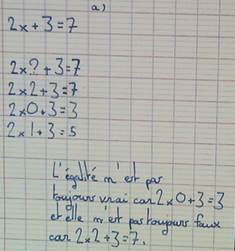 L’élève a senti le besoin de remplacé x par « ? » (alors que cela n’a jamais été fait en classe).  L’élève écrit sa réponse comme les corrections proposées lors des activités flashs. |
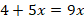 | 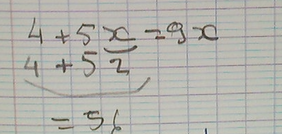 Seul un élève a remplacé la lettre sans faire la multiplication (aucun n’a fait d’addition). 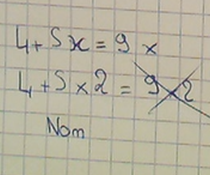 L’élève fait bien des multiplications. |
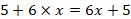 |  L’élève fait les bons calculs, remarque qu’il faudrait essayer tous les nombres, mais ne voit pas comment faire autrement. L’élève a bien compris le principe. |
Ecrire la formule correspondant au programme de calcul suivant :

La difficulté rencontrée par les élèves a été plus la compréhension du programme de calculs qui n’avait pas été assez travaillée en amont. Après des explications sur le fonctionnement voici des écrits d’élèves :
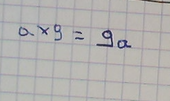

L’élève commence par écrire l’expression sans les signes « × » puis les remets lors de son explication.
L’égalité 2y+6=4(y-1) est-elle vraie pour y=5 ?
C’est la première fois que les élèves sont face à une expression sans signe opératoire devant une parenthèse. Voici les réactions des élèves :
Un quart des élèves disent : « on ne sait pas faire il n’y a pas de signe entre le 4 et la parenthèse »
Un autre quart décide d’additionner.
En ce qui concerne la moitié restante ils disent : « quand il n’y a rien il s’agit d’une multiplication ».
Il nous semble que le passage par l’oral a permis de construire plus solidement ce changement d’écriture : pour la très grande majorité de nos élèves, le passage d’une écriture à l’autre ne pose aucun problème et il leur parait évident qu’il s’agit d’une multiplication, en aucun cas d’une addition. Reste à voir si ce qui semble bien acquis en 5ème va le rester dans le temps.
Amandine Laurent, enseignante au collège Louis Launay - Landivy (53)Angélique Paris, enseignante au collège Louis Launay - Landivy (53)Damien Rivière, enseignant au collège Pierre Dubois - Laval (53)Eric Phocion, enseignant au collège Jean Louis Bernard - Bais(53)Sandra Maulave, enseignante au collège Francis Lallard - Gorron (53)
information(s) pédagogique(s)
niveau : tous niveaux
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA



