espace pédagogique > disciplines du second degré > mathématiques > enseignement > groupes de recherche > TraAM > 2019-2021
modéliser des aires et des volumes
mis à jour le 16/11/2021
mots clés : volume, aire, modélisation, TraAM
Prérequis
- Calculer l'aire de figures usuelles
- Calculer le volume d'un parallélépipède rectangle
- Utiliser une échelle
- Utiliser la proportionnalité
Objectif
Découvrir la modélisation mathématique
Déroulement
Pour chacun des exercices :
- En travail individuel, les élèves prennent connaissance de l'énoncé et écrivent d'éventuelles questions de compréhension.
- L'enseignant répond individuellement ou collectivement aux questions.
- Les élèves cherchent des stratégies de résolution et les mettent en oeuvre. Le rôle de l'enseignant est d'encourager les élèves à chercher et à essayer d'appliquer des idées de modélisation. Il peut choisir de regrouper les élèves en fonction des modèles choisis, notamment en cas de diffculté.
- Du matériel peut être mis à disposition (ordinateurs, quadrillages, ...).
- Des élèves présentent leurs travaux, aboutis ou non, à la classe. Les modèles sont comparés. La précision des résultats et la pertinence des choix réalisés sont discutées.
- La classe écrit un bilan sur ce que peut-être la modélisation.
Plusieurs stratégies devraient être mises en oeuvre par les élèves :
|  |
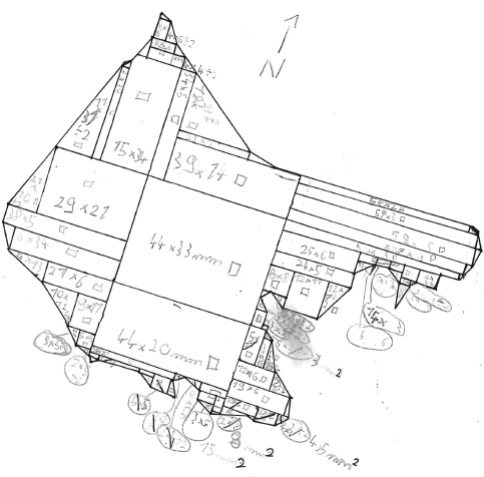
| Cet exercice devrait permettre de discuter de différents types de modélisation : ici la forme peut être modélisée par des figures géométriques usuelles. |  |
| En assimilant la voiture à deux pavés droits et en utilisant la proportionnalité, les élèves devraient trouver des approximations du volume de la voiture relativement proches. |  |
A l'issue des trois exercices, les élèves devraient avoir conscience que le choix du modèle :
- dépend de la forme ;
- influe sur la précision du résultat ;
- détermine la performance de résolution (temps nécessaire, quantité de ressources utilisées).
Du fait des conditions sanitaires (Covid19), aucun matériel n'a été mis à disposition et la plupart des élèves n'ont eu le temps de faire que le premier exercice.
Tous les élèves se sont mis en activité sans trop de diffculté.
Plusieurs modélisations ont été mises en oeuvre par les élèves :
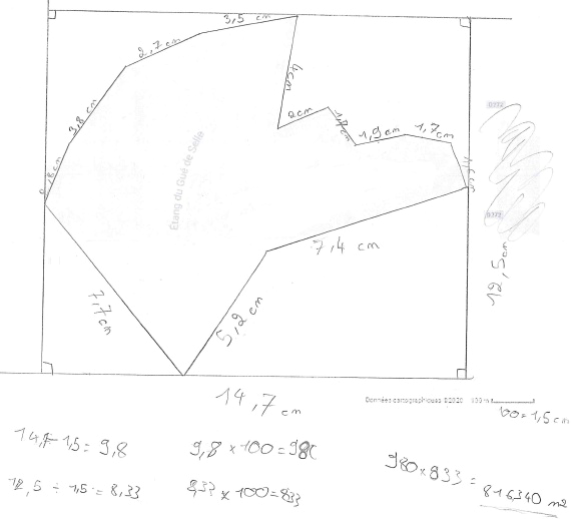
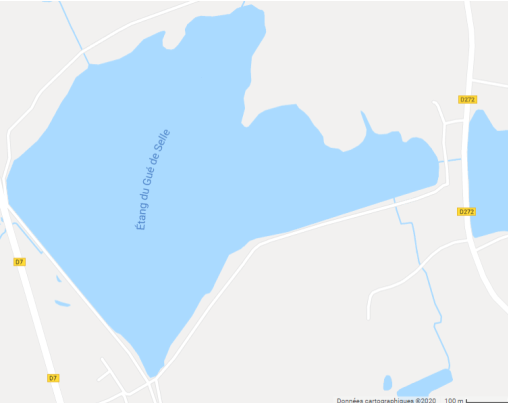
- Encadrement de la surface par un rectangle, dont l'aire est calculée, avant d'être divisée par deux.
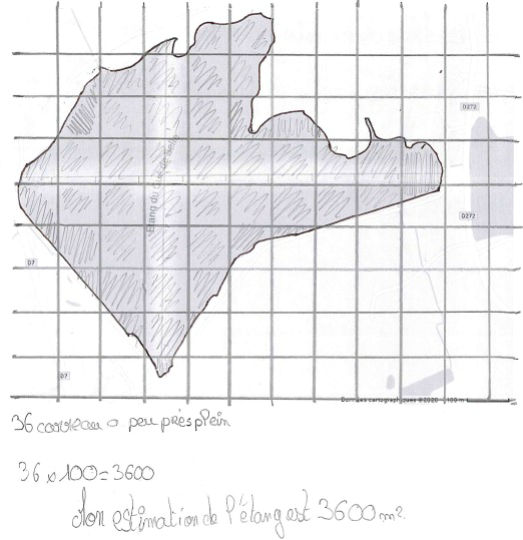
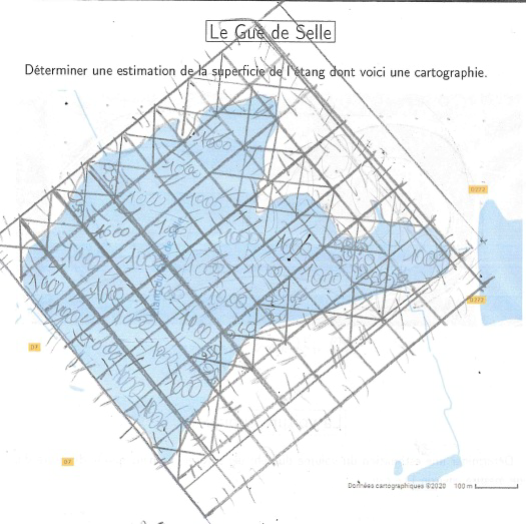
- Utilisation d'un quadrillage dont les côtés mesurent 1, 5 cm ; l'échelle donnée étant 1, 5 cm : 100 m, le nombre de carrés obtenus a ensuite été multiplié par 100.
- Découpage fin de la surface par des figures usuelles et calcul de leurs aires.
Très rapidement, les élèves m'ont fait part d'une difficulté : aucune échelle n'est présente sur le document. Après avoir observé les différents éléments visibles, ils ont choisi collégialement de prendre comme repère la largeur d'une voiture. Je leur ai indiqué que celle-ci mesure environ 2 m.
Tous les élèves ayant abordé cet exercice ont rapidement commencé par tracer un quadrillage.
Je les ai alors questionnés sur l'intérêt de ce quadrillage pour les amener à comprendre que le disque était une forme géométrique plus appropriée dans cet situation. Ils ont ensuite tracé un rectangle pour approximer la partie centrale.

Seul un élève a commencé cet exercice, mais n'a pas eu le temps d'aboutir.
Les élèves ont comparé les diverses méthodes utilisées et discuté de leur efficacité, de leur précision et de leur coût en temps.
Ce travail a également permis de constater que les calculs d'aires, l'utilisation d'une échelle et les conversions d'aires ne sont pas maitrisés par tous.
Sophie Desruelle, enseignantes au collège Paul Langevin, Évron (53)
information(s) pédagogique(s)
niveau : tous niveaux, Collèges tous niveaux, 6ème
type pédagogique :
public visé : non précisé
contexte d'usage :
référence aux programmes :
ressources associées
|
aire d'un étang | 16/11/2021 |
| Modéliser l'aire d'un étang au lycée à partir d'une activité de sixième ! |
||
| aire, modélisation, TraAM | Guillaume François | |
mathématiques - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA