espace pédagogique > actions éducatives > délégation au numérique > pédagogie, innovation
le numérique en mathématiques
mis à jour le 23/10/2012
Les interactions entre activités mathématique et informatique sont multiples et ancrées dans l'histoire depuis déjà plus d'un demi-siècle. La puissance du calcul automatique a modifié de façon profonde l'évolution des mathématiques, permettant en particulier d'augmenter considérablement les potentialités de la recherche et d'aborder des objets sous un jour nouveau. De façon réciproque faire progresser l'informatique génère des problèmes mathématiques nouveaux. Mathématiques et informatique sont donc devenues maintenant indissociables.
mots clés : numérique, programmes, instructions, mathématiques, pédagogie
Pourquoi utiliser le numérique pour enseigner les mathématiques ?
L'enseignement des mathématiques a pour objectif de développer conjointement et progressivement les capacités d'expérimentation et de raisonnement, d'imagination et d'analyse critique. C'est au travers de la résolution de problèmes, de la modélisation de quelques situations et de l'apprentissage progressif de la démonstration, que les élèves prennent conscience petit à petit de ce qu'est une véritable activité mathématique, et acquièrent la pratique d'une démarche scientifique. Or grâce aux spécificités et potentialités qui lui sont propres, le numérique élargit notablement la palette des moyens qui sont à disposition des enseignants et des élèves pour mettre en œuvre les différents aspects de la démarche scientifique et la particularité de sa déclinaison en mathématiques. De plus former à la démarche algorithmique est un objectif de l'enseignement. L'usage du numérique fait donc aujourd'hui partie intégrante de l'enseignement des mathématiques.
L'enseignement des mathématiques a pour objectif de développer conjointement et progressivement les capacités d'expérimentation et de raisonnement, d'imagination et d'analyse critique. C'est au travers de la résolution de problèmes, de la modélisation de quelques situations et de l'apprentissage progressif de la démonstration, que les élèves prennent conscience petit à petit de ce qu'est une véritable activité mathématique, et acquièrent la pratique d'une démarche scientifique. Or grâce aux spécificités et potentialités qui lui sont propres, le numérique élargit notablement la palette des moyens qui sont à disposition des enseignants et des élèves pour mettre en œuvre les différents aspects de la démarche scientifique et la particularité de sa déclinaison en mathématiques. De plus former à la démarche algorithmique est un objectif de l'enseignement. L'usage du numérique fait donc aujourd'hui partie intégrante de l'enseignement des mathématiques.
lu dans les textes officiels
Dans tous les programmes de mathématiques les préconisations sont, à l'instar des enjeux de formation, fortes.
- Au niveau du collège (BO spécial n°6 du 28 Août 2008) l'en-tête commun à tous les programmes explicite :
- Par ailleurs le décret du 11 juillet 2006 relatif au socle commun fait obligation à tout élève de « savoir utiliser des outils ([...] logiciels) » compétence 3 et de « être capable de s'approprier un environnement informatique de travail » compétence 4.
- Au niveau du lycée, les nouveaux programmes précisent les objectifs de formation liés aux outils numériques, par exemple
Un extrait de l'en-tête de ces programmes : « Lors de la résolution de problèmes, l'utilisation de logiciels de calcul formel peut limiter le temps consacré à des calculs très techniques afin de se concentrer sur la mise en place de raisonnements ».
- Dans les BTS pour lesquels le CCF remplace l'épreuve ponctuelle terminale, 30% de l'évaluation porte désormais sur les capacités liées à l'utilisation de logiciels. L'évolution des situations d'évaluation nécessite des étudiants une aptitude à faire preuve d'initiative et d'autonomie dans le choix des potentialités des logiciels à utiliser pour étudier un problème.
En outre, les mathématiques ont aussi comme objectif de construire des compétences spécifiques en informatique. C'est tout particulièrement le cas dans le cadre de la contribution des mathématiques à l'enseignement de spécialité de terminale S, ISN (informatique et sciences du numérique).
Trois modalités d'utilisation des logiciels sont préconisées dans les en-têtes de programmes :
- Au niveau du collège (BO spécial n°6 du 28 Août 2008) l'en-tête commun à tous les programmes explicite :
- « L'utilisation des outils logiciels est particulièrement importante et doit être privilégiée chaque fois qu'elle est une aide à l'imagination, à la formulation de conjectures ou au calcul. »
- Les élèves doivent apprendre en particulier à construire une figure géométrique dans un environnement informatique et réaliser une feuille de calcul adaptée au problème à traiter, et cela de façon autonome.
- Par ailleurs le décret du 11 juillet 2006 relatif au socle commun fait obligation à tout élève de « savoir utiliser des outils ([...] logiciels) » compétence 3 et de « être capable de s'approprier un environnement informatique de travail » compétence 4.
- L'aide à l'imagination que les outils logiciels apportent et la liberté qu'ils procurent en palliant, si besoin est, une maîtrise insuffisante de la technique, qui peut se révéler préjudiciable à l'activité de recherche, sont des leviers très précieux pour permettre à tout élève de construire les attendus du socle commun de connaissances et de compétences.
- Au niveau du lycée, les nouveaux programmes précisent les objectifs de formation liés aux outils numériques, par exemple
- En classe de seconde il s'agit de rendre les élèves capables d' « utiliser les outils logiciels adaptés à la résolution d'un problème » et de « pratiquer une activité expérimentale ou algorithmique » (BO spécial N°30 23 juillet 2009. )
- Dans le cycle terminal, il s'agit de rendre les élèves capables de « chercher, expérimenter, modéliser en particulier à l'aide d'outils logiciels » et de « mettre en œuvre des algorithmes » (BO spécial N°9 30 septembre 2010 pour les séries ES&L, STI2D et S ; BO N°6 9 février 2012 pour la série STMG)
Un extrait de l'en-tête de ces programmes : « Lors de la résolution de problèmes, l'utilisation de logiciels de calcul formel peut limiter le temps consacré à des calculs très techniques afin de se concentrer sur la mise en place de raisonnements ».
- Dans les BTS pour lesquels le CCF remplace l'épreuve ponctuelle terminale, 30% de l'évaluation porte désormais sur les capacités liées à l'utilisation de logiciels. L'évolution des situations d'évaluation nécessite des étudiants une aptitude à faire preuve d'initiative et d'autonomie dans le choix des potentialités des logiciels à utiliser pour étudier un problème.
En outre, les mathématiques ont aussi comme objectif de construire des compétences spécifiques en informatique. C'est tout particulièrement le cas dans le cadre de la contribution des mathématiques à l'enseignement de spécialité de terminale S, ISN (informatique et sciences du numérique).
Trois modalités d'utilisation des logiciels sont préconisées dans les en-têtes de programmes :
- Par le professeur en classe avec un dispositif de visualisation collective
- Par les élèves sous forme de travaux pratiques de mathématiques
- Dans le cadre d'un travail personnel hors de la classe
vu et observé dans la discipline
L'usage des outils numériques permet notamment dans le cadre d'activités de classe :
- d'obtenir rapidement une représentation d'un problème, d'un concept afin de lui donner du sens et de favoriser son appropriation par l'élève ;
- de relier différents aspects (numérique, algébrique, géométrique, algorithmique...) d'un même concept ou d'une même situation ;
d'explorer des situations en faisant apparaître de façon dynamique différentes configurations ;
- d'émettre des conjectures à partir d'une expérimentation interactive lors de l'étude d'un problème comportant des questions ouvertes ou d'une certaine complexité, et de procéder à des premières vérifications ;
- de faire étudier aux élèves des situations plus riches, davantage ancrées dans les différents domaines de leur vie courante, des autres champs disciplinaires ou professionnels étudiés en les dispensant de l'acquisition d'une maîtrise technique excessive ;
- de procéder rapidement à la vérification de certains résultats obtenus.
Quels sont les types d'outils numériques utilisés ?
a) L'usage raisonné de plusieurs types de logiciels par les élèves étant un objectif de formation, leur variété est à cultiver et à étoffer petit à petit.
Au collège, les logiciels de construction géométrique jouent un rôle majeur dans l'apprentissage de la notion de figure géométrique, par l'éclairage nouveau qu'ils donnent aux propriétés des figures. Les tableurs présentent un grand intérêt pour la gestion des données nombreuses (nécessaires pour offrir des situations qui font sens). Ils représentent un outil didactique particulièrement performant pour l'apprentissage de l'algèbre. Les logiciels de calcul formel peuvent accompagner utilement certaines résolutions de problème.
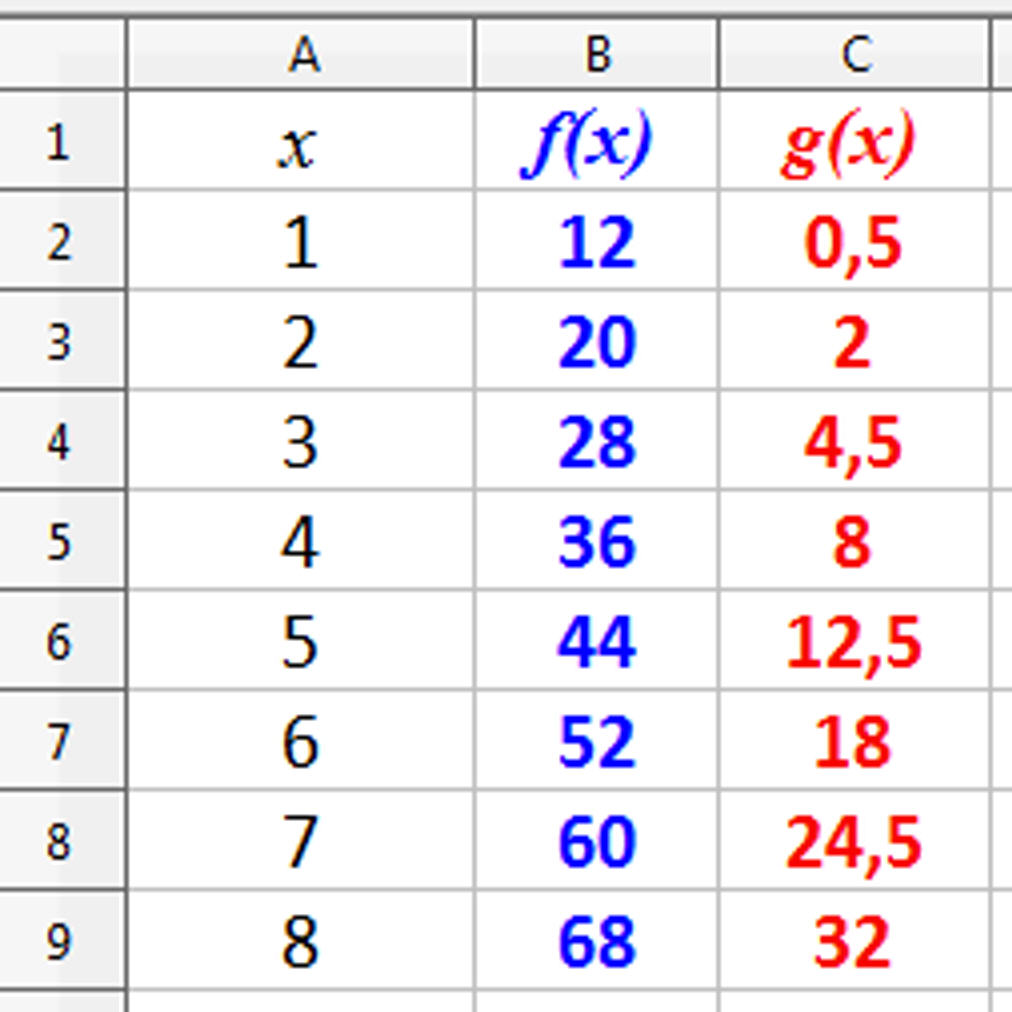
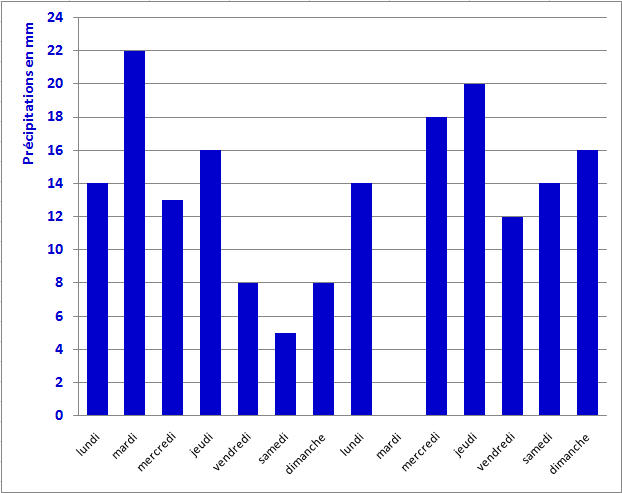
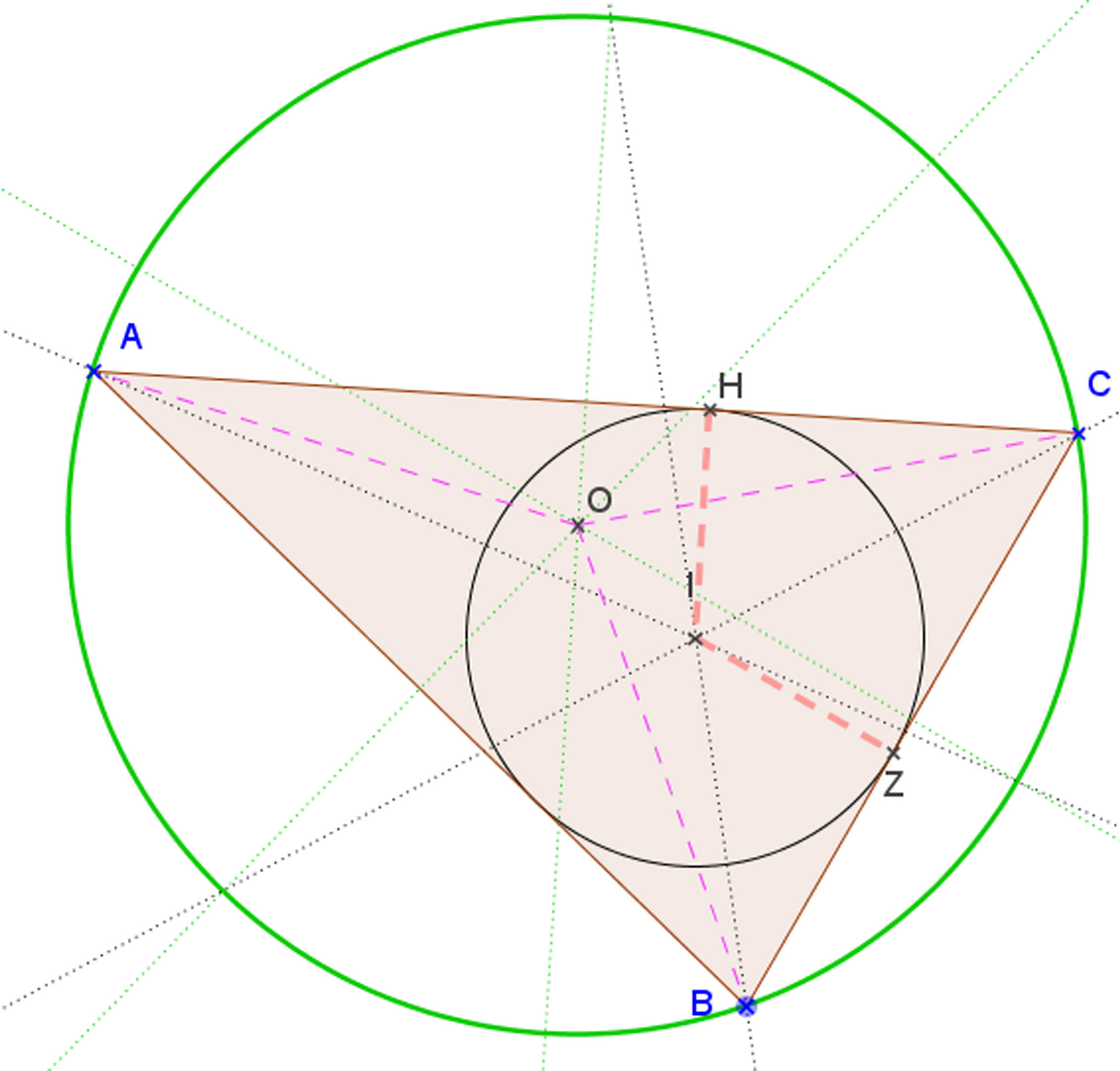
Au lycée, la palette des logiciels mis à disposition de l'activité mathématique des élèves s'élargit encore. Outre des logiciels de construction géométrique et un tableur, les élèves doivent pouvoir mobiliser de façon autonome un traceur de courbes, et se familiariser à d'autres outils tels qu'un logiciel de calcul formel, un logiciel comprenant toutes les fonctions statistiques et lois de probabilité au programme et un logiciel de programmation. Par ailleurs dans les séries technologiques et en BTS, il est recommandé que, dans le cadre de leur formation en mathématiques, les élèves aient l'occasion de se servir des logiciels les plus fréquemment utilisés dans les disciplines qui donnent sa couleur à la voie de formation.
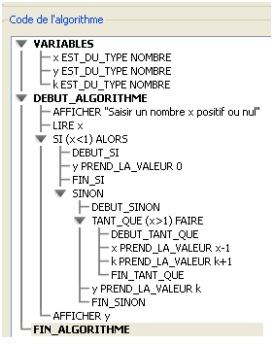
b) Au-delà des outils logiciels mis à disposition des élèves, certains matériels et ressources numériques sont utilisés pour mettre en œuvre les pratiques pédagogiques adaptées à l'enseignement des mathématiques, voire innovantes, qui permettent de répondre aux exigences des programmes :
- ordinateur relié à un vidéo-projecteur éventuellement couplé à une caméra de visualisation numérique et/ou un tableau numérique interactif ;
- émulateur de calculatrice,
- manuel numérique ;
- accès à Internet (recherche documentaire, énigmes, jeux et concours en ligne, logiciels en ligne).
c) Enfin, certains services numériques en ligne permettent aux enseignants des pratiques nouvelles tout à fait adaptées à l'enseignement des mathématiques :
l'Espace Numérique de Travail (e-lyco pour l'académie de Nantes) rend possibles des échanges personnalisés entre élèves ou entre le professeur et des élèves. Il contribue à une différenciation de la pédagogie en permettant la mise à disposition des élèves de ressources pédagogiques variées, le suivi de travaux personnalisés et différenciés à distance via le cahier de texte numérique, la mise à disposition d'entrainements ciblés. L'ENT peut en cela s'apparenter à un vrai « cahier virtuel » constitué de ressources qui font sens pour l'élève car utilisées en classe ou complémentaires à ce qui a été fait en classe. L'ENT facilite aussi la mutualisation des ressources entre professeurs (riche de retombées positives sur le travail en équipe) et la récupération des « copies numériques » déposées en ligne par les élèves (favorable aux échanges fructueux élève-professeur).
Quels sont les contextes d'usages des outils numériques ?
On peut distinguer aujourd'hui quatre contextes d'usages des outils numériques dans l'enseignement des mathématiques :
a) Utilisation en classe d'un poste unique couplé à un vidéoprojecteur
L'utilisation en classe par le professeur, ou par un élève qui « pilote au clavier ». Cet usage a de nombreux avantages :
- montrer au cours d'une séance que certains outils logiciels sont particulièrement bien adaptés à la résolution de certains problèmes mathématiques ;
- intégrer clairement cet usage à l'apprentissage des mathématiques (il n'y a pas les mathématiques que l'on fait en classe et d'autres bien différentes que l'on ne ferait qu'en salle informatique) ;
- faire découvrir dans un cadre collectif aux élèves l'utilisation de certaines fonctionnalités des logiciels, au travers de la résolution d'une question mathématique (cette approche collective se révèle bien souvent un bon moyen pour que l'élève, seul face à un ordinateur, puisse à son tour commencer à utiliser les différents outils et elle s'avère également adaptée pour introduire ensuite des fonctionnalités plus complexes des logiciels) ;
- offrir des visualisations concrètes facilitant l'appropriation de certaines notions ;
- faciliter l'exploitation des productions des élèves en offrant la possibilité d'en avoir une visualisation collective ;
- permettre l'élaboration collective et la diversification des traces avec lesquelles les élèves peuvent retravailler après la classe.
b) Utilisation en classe de postes informatiques (éventuellement mobiles)
L'utilisation par les élèves eux-mêmes, et à leur initiative, des outils numériques afin de résoudre les problèmes et les activités qui leur sont proposés en cours de mathématiques. Rendre les élèves capables de faire preuve d'initiative et d'autonomie dans l'utilisation de ces outils nécessite leur accessibilité : présence de postes en « fond de classe » ou disponibilité d'une « classe mobile »
c) Utilisation en « salle informatique » ou « salle multimédia »
Dans le cadre des Travaux Pratiques de mathématiques qui sont à proposer, les élèves doivent pouvoir mobiliser par eux-mêmes les outils numériques qui leur sont familiers pour étudier un problème. De telles séances permettent de développer et de travailler un grand nombre des compétences attendues. Les élèves peuvent alors être à deux ou seuls par poste, une moitié de classe faisant par exemple un travail sur table avec permutation en milieu de séance.
d) Utilisation hors du temps d'enseignement
Proposer des travaux personnels individualisés, pour lesquels le recours aux outils numériques est possible et autorisé, est un autre moyen utilisé par les professeurs de tendre vers un usage autonome de ces outils par l'élève pour faire des mathématiques. Cela permet aussi à des élèves de consolider certains apprentissages, à d'autres d'aller plus loin. Le taux d'équipement, toujours croissant, des familles peut encourager ces pratiques, mais les établissements doivent assurer des conditions essentielles d'égalité des chances en rendant possible l'accès à des ordinateurs au sein de l'établissement (CDI, salle informatique, salle de mathématiques...).
Les réseaux d'établissement et les ENT sont particulièrement précieux pour prolonger les travaux engagés lors des séances avec l'enseignant et faciliter les échanges à distance entre le professeur et ses élèves.
- d'obtenir rapidement une représentation d'un problème, d'un concept afin de lui donner du sens et de favoriser son appropriation par l'élève ;
- de relier différents aspects (numérique, algébrique, géométrique, algorithmique...) d'un même concept ou d'une même situation ;
d'explorer des situations en faisant apparaître de façon dynamique différentes configurations ;
- d'émettre des conjectures à partir d'une expérimentation interactive lors de l'étude d'un problème comportant des questions ouvertes ou d'une certaine complexité, et de procéder à des premières vérifications ;
- de faire étudier aux élèves des situations plus riches, davantage ancrées dans les différents domaines de leur vie courante, des autres champs disciplinaires ou professionnels étudiés en les dispensant de l'acquisition d'une maîtrise technique excessive ;
- de procéder rapidement à la vérification de certains résultats obtenus.
Quels sont les types d'outils numériques utilisés ?
a) L'usage raisonné de plusieurs types de logiciels par les élèves étant un objectif de formation, leur variété est à cultiver et à étoffer petit à petit.
Au collège, les logiciels de construction géométrique jouent un rôle majeur dans l'apprentissage de la notion de figure géométrique, par l'éclairage nouveau qu'ils donnent aux propriétés des figures. Les tableurs présentent un grand intérêt pour la gestion des données nombreuses (nécessaires pour offrir des situations qui font sens). Ils représentent un outil didactique particulièrement performant pour l'apprentissage de l'algèbre. Les logiciels de calcul formel peuvent accompagner utilement certaines résolutions de problème.



Au lycée, la palette des logiciels mis à disposition de l'activité mathématique des élèves s'élargit encore. Outre des logiciels de construction géométrique et un tableur, les élèves doivent pouvoir mobiliser de façon autonome un traceur de courbes, et se familiariser à d'autres outils tels qu'un logiciel de calcul formel, un logiciel comprenant toutes les fonctions statistiques et lois de probabilité au programme et un logiciel de programmation. Par ailleurs dans les séries technologiques et en BTS, il est recommandé que, dans le cadre de leur formation en mathématiques, les élèves aient l'occasion de se servir des logiciels les plus fréquemment utilisés dans les disciplines qui donnent sa couleur à la voie de formation.



b) Au-delà des outils logiciels mis à disposition des élèves, certains matériels et ressources numériques sont utilisés pour mettre en œuvre les pratiques pédagogiques adaptées à l'enseignement des mathématiques, voire innovantes, qui permettent de répondre aux exigences des programmes :
- ordinateur relié à un vidéo-projecteur éventuellement couplé à une caméra de visualisation numérique et/ou un tableau numérique interactif ;
- émulateur de calculatrice,
- manuel numérique ;
- accès à Internet (recherche documentaire, énigmes, jeux et concours en ligne, logiciels en ligne).
c) Enfin, certains services numériques en ligne permettent aux enseignants des pratiques nouvelles tout à fait adaptées à l'enseignement des mathématiques :
l'Espace Numérique de Travail (e-lyco pour l'académie de Nantes) rend possibles des échanges personnalisés entre élèves ou entre le professeur et des élèves. Il contribue à une différenciation de la pédagogie en permettant la mise à disposition des élèves de ressources pédagogiques variées, le suivi de travaux personnalisés et différenciés à distance via le cahier de texte numérique, la mise à disposition d'entrainements ciblés. L'ENT peut en cela s'apparenter à un vrai « cahier virtuel » constitué de ressources qui font sens pour l'élève car utilisées en classe ou complémentaires à ce qui a été fait en classe. L'ENT facilite aussi la mutualisation des ressources entre professeurs (riche de retombées positives sur le travail en équipe) et la récupération des « copies numériques » déposées en ligne par les élèves (favorable aux échanges fructueux élève-professeur).
Quels sont les contextes d'usages des outils numériques ?
On peut distinguer aujourd'hui quatre contextes d'usages des outils numériques dans l'enseignement des mathématiques :
a) Utilisation en classe d'un poste unique couplé à un vidéoprojecteur
L'utilisation en classe par le professeur, ou par un élève qui « pilote au clavier ». Cet usage a de nombreux avantages :
- montrer au cours d'une séance que certains outils logiciels sont particulièrement bien adaptés à la résolution de certains problèmes mathématiques ;
- intégrer clairement cet usage à l'apprentissage des mathématiques (il n'y a pas les mathématiques que l'on fait en classe et d'autres bien différentes que l'on ne ferait qu'en salle informatique) ;
- faire découvrir dans un cadre collectif aux élèves l'utilisation de certaines fonctionnalités des logiciels, au travers de la résolution d'une question mathématique (cette approche collective se révèle bien souvent un bon moyen pour que l'élève, seul face à un ordinateur, puisse à son tour commencer à utiliser les différents outils et elle s'avère également adaptée pour introduire ensuite des fonctionnalités plus complexes des logiciels) ;
- offrir des visualisations concrètes facilitant l'appropriation de certaines notions ;
- faciliter l'exploitation des productions des élèves en offrant la possibilité d'en avoir une visualisation collective ;
- permettre l'élaboration collective et la diversification des traces avec lesquelles les élèves peuvent retravailler après la classe.
b) Utilisation en classe de postes informatiques (éventuellement mobiles)
L'utilisation par les élèves eux-mêmes, et à leur initiative, des outils numériques afin de résoudre les problèmes et les activités qui leur sont proposés en cours de mathématiques. Rendre les élèves capables de faire preuve d'initiative et d'autonomie dans l'utilisation de ces outils nécessite leur accessibilité : présence de postes en « fond de classe » ou disponibilité d'une « classe mobile »
c) Utilisation en « salle informatique » ou « salle multimédia »
Dans le cadre des Travaux Pratiques de mathématiques qui sont à proposer, les élèves doivent pouvoir mobiliser par eux-mêmes les outils numériques qui leur sont familiers pour étudier un problème. De telles séances permettent de développer et de travailler un grand nombre des compétences attendues. Les élèves peuvent alors être à deux ou seuls par poste, une moitié de classe faisant par exemple un travail sur table avec permutation en milieu de séance.
d) Utilisation hors du temps d'enseignement
Proposer des travaux personnels individualisés, pour lesquels le recours aux outils numériques est possible et autorisé, est un autre moyen utilisé par les professeurs de tendre vers un usage autonome de ces outils par l'élève pour faire des mathématiques. Cela permet aussi à des élèves de consolider certains apprentissages, à d'autres d'aller plus loin. Le taux d'équipement, toujours croissant, des familles peut encourager ces pratiques, mais les établissements doivent assurer des conditions essentielles d'égalité des chances en rendant possible l'accès à des ordinateurs au sein de l'établissement (CDI, salle informatique, salle de mathématiques...).
Les réseaux d'établissement et les ENT sont particulièrement précieux pour prolonger les travaux engagés lors des séances avec l'enseignant et faciliter les échanges à distance entre le professeur et ses élèves.
Les investissements des collectivités territoriales ont permis une plus grande disponibilité des outils numériques dans les établissements scolaires et ont d'ores et déjà métamorphosé l'activité proposée aux élèves dans le cadre de l'enseignement des mathématiques. Sans doute peut-on encore faire encore mieux mais l'activité mathématique des élèves se révèle quotidiennement déjà beaucoup plus riche, plus variée et plus dynamique qu'il y a ne serait-ce qu'une dizaine d'années. Les professeurs sont à présent conscients de toutes les potentialités nouvelles qui s'offrent à eux et ils sont engagés et volontaires pour se les approprier pleinement dans l'intérêt de la formation des élèves qui leur sont confiés.
Stéphane Percot, IATICE de mathématiques
contributeur(s) :Françoise Munck, IA-IPR de mathématiques
numérique et enseignement - Rectorat de l'Académie de Nantes

 s'identifier
s'identifier
 portail personnel ETNA
portail personnel ETNA
