numérique et enseignement

En mathématiques, les   outils   numériques   (tableur,   logiciel   de   géométrie   dynamique,   calcul   formel,   logiciel   de programmation) libèrent l’activité des élèves en augmentant la palette des stratégies possibles pour étudier un problème et en trouver une solution, même si cette dernière n’est parfois qu’approchée. En cela, le numérique peut être un vecteur efficace de différenciation.  

Certains problèmes peuvent être entièrement résolus par des outils numériques (ex : recherche sur tableur d’un problème comportant un nombre fini de possibilités). D’autres encore, ne peuvent être traités qu’algorithmiquement. 
Voir activité « comptons les points ! ».

On oppose parfois les méthodes « purement mathématiques » ou devrais-je dire « mathématiquement pures » de résolution d’un problème avec les stratégies utilisant les outils numériques pour chercher, tester, tâtonner. En particulier dans le domaine algébrique, on oppose parfois la stratégie de résolution d’un problème utilisant des équations aux méthodes utilisant les logiciels de calcul (type tableur).

Cependant  l’utilisation  de  formules tableur  constitue  souvent un premier  pas  vers  la  construction de  formules  algébriques.  Par  ailleurs pouvoir  tester  sur  beaucoup  de  nombres,  deux  programmes  de  calcul  différents,  pouvoir  affiner  le pas  pour  approcher  celui  ou  ceux  qui  permettent  d’obtenir,  avec  les  deux  programmes,  le  même résultat  est  une  stratégie  pédagogique  efficace  pour  faire  comprendre  aux  élèves  le  sens  nouveau que prend le symbole « égal » dans une équation.

Toujours sur la thématique de l’expertise calculatoire, on peut s’interroger sur le rôle que peut jouer le calcul formel dans l’acquisition d’une maîtrise des techniques algébriques.

Il  est  important  que  le  recours  au  calcul  formel  ne  soit  pas  systématique  (comme  l’utilisation  de  la calculatrice dans le cadre de l’apprentissage du calcul numérique).  Quand la situation étudiée n’exige  qu’un niveau de maîtrise technique abordable, un calcul algébrique réalisé à la main est toujours un attendu. Toutefois l’expérience conduite en lycée tendrait à prouver que seuls les élèves qui ont déjà construit une certaine maitrise algébrique y ont recours spontanément. L’utilisation du calcul formel n’empêche pas la mobilisation chez l’élève de l’intelligence du calcul mais tout au contraire la favorise.  Choisir la forme de l’expression algébrique adaptée à la question  reste  toujours  de  l’autonomie  de  l’élève.  Cette  mise  à  disposition  d’un  logiciel  de  calcul formel  ne  nous  semble  donc  pas  opposée  à  la  volonté  d’aller  vers  une  meilleure  maîtrise  des techniques algébriques par les élèves mais constitue un outil à intégrer dans le cadre d’une différenciation pédagogique.

D’une  manière  générale,  les  outils  numériques  offrent  dans  de  nombreux  cadres  une  piste  de différenciation pour mettre en œuvre les activités proposées aux élèves.

 

Exemple 1 : pour résoudre un problème de calcul pouvant se ramener à une équation du premier degré (classe de 4ème)
Un livre coûte 5 € de moins qu’un CD et un jeu vidéo coûte le double d’un CD. Arthur achète 4 livres, 1 CD et 2 jeux pour un total de 80,80 €. Quel est le prix d’un CD ? D’un livre ? D’un jeu vidéo ?
Pour certains élèves ayant déjà une bonne maitrise algébrique, la mise en équation et la résolution algébrique de ce problème ne pose pas de souci.

 


 

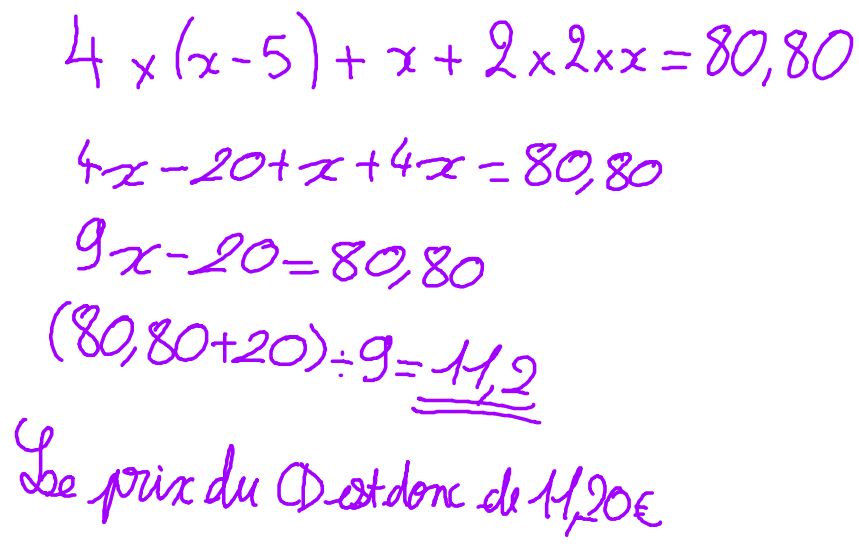
Pour d’autres, la stratégie par essai-erreur peut le permettre de trouver la solution.

 
 

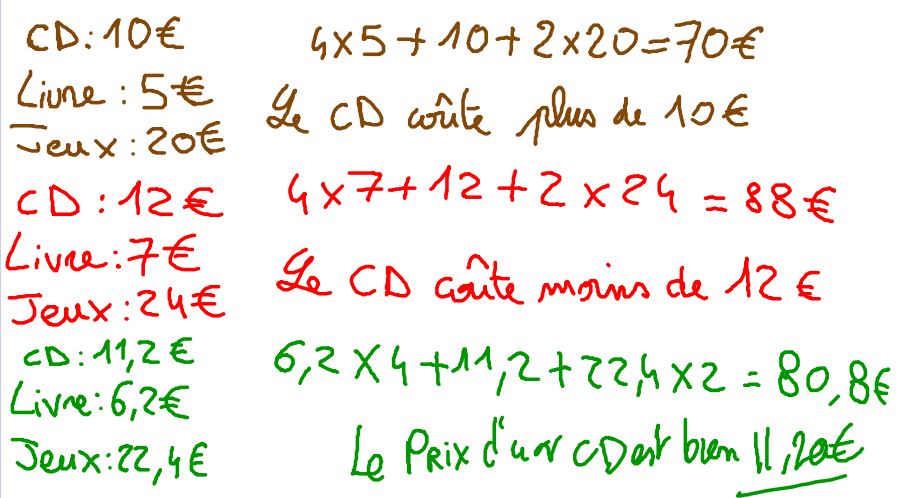
Le tableur peut être un outil intéressant pour faciliter les calculs mais aussi pour faire un pas vers l’algébrisation du problème.

 

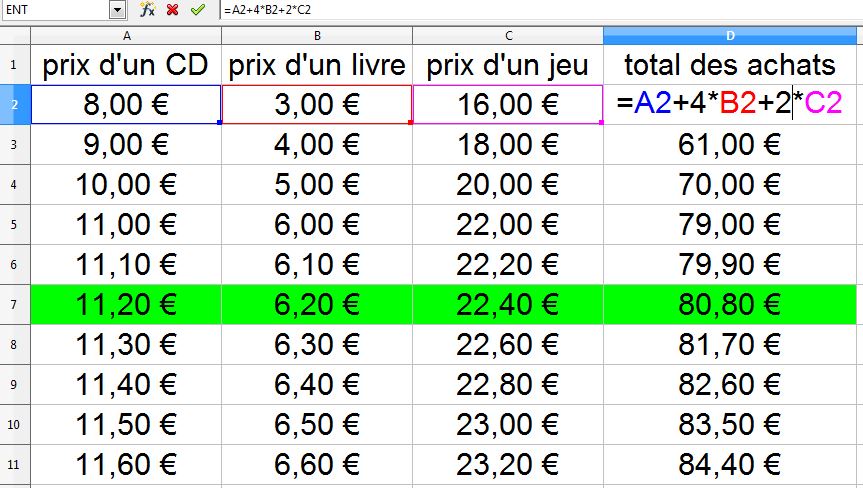
Le tableur apparait ici comme une passerelle vers l’algébrisation. Il constitue un outil précieux de différenciation dans la résolution de ce problème et dans l’apprentissage de l’algèbre.
L’élève qui est capable de comprendre et utiliser la programmation des cellules (par exemple = A2+4*B2+2*C2), fait un pas vers l’algébrisation : x + 4y + 2z ….

Exemple 2 : pour résoudre le problème géométrique de Varignon
Soit RSTU un quadrilatère quelconque.
Les points A, B, C et D sont les milieux respectifs des côtés [RS], [ST], [TU] et [UR].
a) Quelle semble être la nature du quadrilatère ABCD ?
b) Quelle(s) condition(s) doit-on avoir au départ sur le quadrilatère RSTU pour que ABCD soit un rectangle ?
c) Quelle(s) condition(s) doit-on avoir au départ sur le quadrilatère RSTU pour que ABCD soit un losange ?
d) Quelle(s) condition(s) doit-on avoir au départ sur le quadrilatère RSTU pour que ABCD soit un carré ?

 

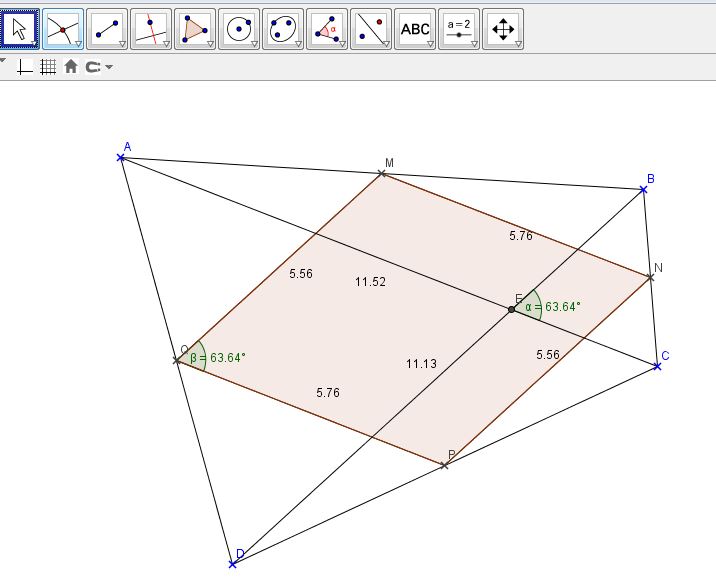
L’utilisation de géogébra permet aux élèves d’explorer différentes configurations et peut nourrir son raisonnement.
Pour certains élèves, il constitue un passage intéressant pour la résolution de ce problème.

 

A découvrir aussi : deux illustrations qui s'inscrivent dans le cadre plus large d'une différenciation basée sur l'oral avec des outils numériques utilisés en mathématiques .

Expérimentation n°1 : au collège Collège Maryse Bastié de Dole dans le Jura :
Objectif : Développer la pratique de l’oral en mathématiques, notamment en s’appuyant sur des outils numériques (M.P.3), pour faciliter la prise d’initiative, la remédiation, et pour évaluer les élèves, en particulier dans le cadre du socle commun.
http://www.ac-besancon.fr/download.php?pdf=IMG/pdf/bilan_2014_clg_bastie_dole.pdf

Expérimentation n°2 : au collège Collège Château-Rance de Scey-sur-Saône   
Objectif : Développer la pratique de l’oral en mathématiques, pour améliorer les compétences des élèves en maîtrise de la langue (orale et écrite), différencier les approches pédagogiques (prise en compte de besoins spécifiques) et évaluer les élèves, notamment dans le cadre du socle commun.
http://www.ac-besancon.fr/download.php?pdf=IMG/pdf/bilan-exp-article34-2014-chateau-rance.pdf